1. In 1933, the astronomer Fritz Zwicky is observing a cluster of gravitationally bound galaxies called the Coma cluster.
a) First, consider a spherical distribution of matter of uniform density \(\rho\), mass M, and radius R. Show that the potential energy U, is given by \[U=-\frac{3GM^2}{5R}.\]
We start with the general equation for gravitational potential energy: \(U=-\frac{GMm}{r}\).
We know the density of the matter is \(\rho\), so we can figure out the mass: \(M=\rho\frac{4}{3}\pi r^3\).
The mass of the infinitesimal piece of collapsing mass is \(dM=\rho4\pi r^2dr\), which allows us to calculate the infinitesimal amount of potential energy contributed by that piece of mass.
\(dU=-\frac{G(\rho\frac{4}{3}\pi r^3)(\rho4\pi r^2dr)}{r}=-\frac{16G\rho^2\pi^2r^4}{3}dr\)
Finally we just have to integrate.
\(\int^U_0dU=-\frac{16G\rho^2\pi^2}{3}\int^R_0r^4dr\)
\(U=-\frac{3G\rho^2\pi^2}{3}\frac{R^5}{5}\)
If we make the substitution \(\rho=\frac{M}{\frac{4}{3}\pi r^3}\), we can simplify to the final answer: \(U=-\frac{3GM^2}{5R}\).
b) The Coma cluster is approximately 1 million light years across (~1024cm). The Coma cluster consists of some ~800 galaxies, each with mass ~109 solar masses. What is the gravitational potential energy of the cluster?
\(U=-\frac{3(6.67\times10^{-8}\frac{cm^3}{s^2g})(800\times10^9\times2\times10^{33}g)^2}{5\times0.5\times10^{24}cm}=-4.1\times10^{59}erg\)
c) By the Virial theorem, what should be the typical velocity of a galaxy in this system?
Using the Virial theorem, we can say that \(\frac{1}{2}mv^2=-\frac{1}{2}U\).
\(\frac{1}{2}Mv^2=\frac{1}{2}\frac{3GM^2}{5R}\)
\(v=(\frac{3GM}{5R})^{1/2}\)
\(v=(\frac{3(6.67\times10^{-8}\frac{cm^3}{s^2g})(800\times10^9\times2\times10^{33}g)}{5\times0.5\times10^{24}cm})^{1/2}=1.1\times10^7cm/s=110km/s\)
d) Fritz Zwicky measured the Doppler shifts of the galaxies in the Coma cluster, and found that the typical velocity exceeds 1000km/s! Knowing what you know of the Virial theorem, and realizing that the mass M we calculated only took account of matter that we can see (galaxies), what is one probable cause of this discrepancy?
It's likely that this discrepancy is caused by dark matter. If we use the Virial theorem to calculate the velocity but we use a mass that's too low, we'll end up with a velocity that's too low--which is what happened here. If there's a large amount of matter that we can't see, that could explain why our mass and our velocity are too low.
Monday, February 29, 2016
Week 5: Sounds...in Space!
This weekend as I was wasting time on Buzzfeed, I found myself looking at an article (probably a generous term for anything on Buzzfeed, actually) about noises in space. This particular list included a few legitimate sounds (a rocket launch, a descent through Titan's atmosphere), but was mostly made up of other types of signals that had been converted to something that we as humans can hear. For example, one "sound" is the conversion of vibrational signals from the Philae lander's touchdown on a comet, and another particularly trippy noise is the slo-mo interaction between solar wind and Saturn's magnetic field.
While most people know that sound doesn't travel in a vacuum, that doesn't stop filmmakers. The sounds of TIE Fighters and space weapons in Star Wars are famous, for instance, despite being totally unrealistic. It makes sense from a filmography standpoint--silence can build suspense, but it has more trouble expressing the intensity of a space battle. If space battles were ever to become a reality, these sounds would probably have to be synthesized by a computer based on other information--sort of like most of the sounds in the Buzzfeed article.
It's interesting to think about whether there was a time when sound in space wasn't such an impossibility. The ability of sound to propagate through a fluid (liquid, gas, or plasma) is dependent on the fluid's density and compressibility. As cosmology teaches us, the Universe went from really-really-ridiculously dense at its inception to not-all-that-dense now, which means that it necessarily passed through a period of sort-of-normal-Earth-atmosphere density (all technical terms, of course). I don't know how early in the Universe's life this was or how long it lasted, but it's possible that the Universe was once a very noisy place.
Sources:
http://www.buzzfeed.com/alexkasprak/cool-ass-space-noises-that-will-make-you-feel-like-an-astron
https://soundcloud.com/nasa/cassini-saturn-radio-emissions-2
https://www.youtube.com/watch?v=T_OSeRxhGOY
https://en.wikipedia.org/wiki/Speed_of_sound#Dependence_on_the_properties_of_the_medium
http://57.media.tumblr.com/be7ebf9987a76f4dc337894f8355c641/tumblr_mtdq4muTvC1rth2h5o2_400.gif
https://www.grc.nasa.gov/www/k-12/airplane/state.html
While most people know that sound doesn't travel in a vacuum, that doesn't stop filmmakers. The sounds of TIE Fighters and space weapons in Star Wars are famous, for instance, despite being totally unrealistic. It makes sense from a filmography standpoint--silence can build suspense, but it has more trouble expressing the intensity of a space battle. If space battles were ever to become a reality, these sounds would probably have to be synthesized by a computer based on other information--sort of like most of the sounds in the Buzzfeed article.
It's interesting to think about whether there was a time when sound in space wasn't such an impossibility. The ability of sound to propagate through a fluid (liquid, gas, or plasma) is dependent on the fluid's density and compressibility. As cosmology teaches us, the Universe went from really-really-ridiculously dense at its inception to not-all-that-dense now, which means that it necessarily passed through a period of sort-of-normal-Earth-atmosphere density (all technical terms, of course). I don't know how early in the Universe's life this was or how long it lasted, but it's possible that the Universe was once a very noisy place.
 |
| *Insert TIE Figher screech* |
Sources:
http://www.buzzfeed.com/alexkasprak/cool-ass-space-noises-that-will-make-you-feel-like-an-astron
https://soundcloud.com/nasa/cassini-saturn-radio-emissions-2
https://www.youtube.com/watch?v=T_OSeRxhGOY
https://en.wikipedia.org/wiki/Speed_of_sound#Dependence_on_the_properties_of_the_medium
http://57.media.tumblr.com/be7ebf9987a76f4dc337894f8355c641/tumblr_mtdq4muTvC1rth2h5o2_400.gif
https://www.grc.nasa.gov/www/k-12/airplane/state.html
Sunday, February 28, 2016
Week 5: WS9 #2
2. Let's apply the equation of hydrostatic equilibrium \[\frac{dP}{dr}=-\rho(r)g(r)\]to some basic physical problems.
a) Imagine a tank/lake/bathtub/ocean on Earth filled with water. Use the equation of hydrostatic equilibrium to prove that the pressure at a depth h is given by \[P(h)=\rho gh+P_{atm}\]where g is the gravitational field of the Earth and Patm is the atmospheric pressure.
\(\frac{dP}{dr}=-\rho g\)
\(\int^{P(h)}_{P_{atm}}dP=\int^0_h-\rho gdr\)
Integrating this expression gives us \(P(h)=\rho gh+P_{atm}\).
b) Noting that on Earth the atmospheric pressure is \(P_{atm}\approx10^6dyne/cm^2\) and that water density is 1g/cc, how many times atmospheric pressure is the pressure at the bottom of the Marianas trench (11km deep)?
\(P_{marianas}=\rho gh=(1g/cm^3)(980cm/s^2)(1.1\times10^6cm)\approx10^9dyne/cm^2\)
\(\frac{P_{marianas}}{P_{atm}}=\frac{10^9}{10^6}=10^3\)
The pressure in the Marianas trench is about 1000 times that on the Earth's surface.
c) Now let us explore what is called the isothermal atmosphere model. In this model, the atmosphere of the Earth is at temperature T that is independent of height. Use the equation of hydrostatic equilibrium and the ideal gas law, P = nkT, where n is the number density of particles and \(k=1.4\times10^{-16}erg/K\) is the Boltzmann constant to derive an expression describing how the density of the Earth's atmosphere varies with height \(\rho(r)\). You may assume the typical mass of particles in the air to have mass m and the density at the Earth's surface is \(\rho_0\).
\(n=\frac{P}{kT}\)
Multiplying both sides by the particle's mass gives us \(mn=\rho=\frac{mP}{kT}\).
Differentiating both sides gives us \(d\rho=\frac{mdP}{kT}=\frac{m}{kT}(-\rho(r)g(r)dr\).
We can approximate g(r) as constant, so the integral becomes \(\int^{\rho(r)}_{\rho_0}\frac{d\rho}{\rho(r)}=\frac{-m}{kT}\int^{r+r_\oplus}_{r_\oplus}gdr\).
Solving and simplifying the integral yields \(\rho(r)=\rho_0e^{\frac{-mgr}{kT}}\).
d) The height, H, over which the density falls off by a factor of 1/e, \[H=\frac{kT}{mg}\]where m is the mean mass of a gas particle, is called the scale height. When astronomers talk about the "thickness" of an atmosphere, we typically mean the scale height of the atmosphere. While formally the solution is defined even when r goes to infinity, atmospheres with greater scale height are "puffier" than those with smaller scale height. What should happen when you increase/decrease m, T, and g?
Looking at the units of H, we can tell that it's actually a height: \([H]=\frac{[dyne\times cm/K][K]}{[g][cm/s^2}=cm\), since \(dyne=\frac{erg}{cm}=\frac{g\times cm}{s^2}\).
This equation indicates that at higher temperatures, the atmosphere should be "puffier." This makes sense, since at higher temperatures the atmospheric gas will expand. With greater values of m (average particle mass) or g, the atmosphere will have a lower scale height. This makes sense, because heavier particles or stronger gravity will result in gas that stays closer to the planet.
e) What is the Earth's scale height, \(H_\oplus\)? The mass of a proton is \(1.7\times10^{-24}g\), and the Earth's atmosphere is mostly molecular nitrogen, N2. Take the average temperature for Earth's atmosphere to be ~250K.
\(H_\oplus=\frac{(1.4\times10^{-16}erg/K)(250K)}{28\times1.7\times10^{-24}g)(980cm/s^2)}=7.5\times10^5cm=7.5km\)
a) Imagine a tank/lake/bathtub/ocean on Earth filled with water. Use the equation of hydrostatic equilibrium to prove that the pressure at a depth h is given by \[P(h)=\rho gh+P_{atm}\]where g is the gravitational field of the Earth and Patm is the atmospheric pressure.
\(\frac{dP}{dr}=-\rho g\)
\(\int^{P(h)}_{P_{atm}}dP=\int^0_h-\rho gdr\)
Integrating this expression gives us \(P(h)=\rho gh+P_{atm}\).
b) Noting that on Earth the atmospheric pressure is \(P_{atm}\approx10^6dyne/cm^2\) and that water density is 1g/cc, how many times atmospheric pressure is the pressure at the bottom of the Marianas trench (11km deep)?
\(P_{marianas}=\rho gh=(1g/cm^3)(980cm/s^2)(1.1\times10^6cm)\approx10^9dyne/cm^2\)
\(\frac{P_{marianas}}{P_{atm}}=\frac{10^9}{10^6}=10^3\)
The pressure in the Marianas trench is about 1000 times that on the Earth's surface.
c) Now let us explore what is called the isothermal atmosphere model. In this model, the atmosphere of the Earth is at temperature T that is independent of height. Use the equation of hydrostatic equilibrium and the ideal gas law, P = nkT, where n is the number density of particles and \(k=1.4\times10^{-16}erg/K\) is the Boltzmann constant to derive an expression describing how the density of the Earth's atmosphere varies with height \(\rho(r)\). You may assume the typical mass of particles in the air to have mass m and the density at the Earth's surface is \(\rho_0\).
\(n=\frac{P}{kT}\)
Multiplying both sides by the particle's mass gives us \(mn=\rho=\frac{mP}{kT}\).
Differentiating both sides gives us \(d\rho=\frac{mdP}{kT}=\frac{m}{kT}(-\rho(r)g(r)dr\).
We can approximate g(r) as constant, so the integral becomes \(\int^{\rho(r)}_{\rho_0}\frac{d\rho}{\rho(r)}=\frac{-m}{kT}\int^{r+r_\oplus}_{r_\oplus}gdr\).
Solving and simplifying the integral yields \(\rho(r)=\rho_0e^{\frac{-mgr}{kT}}\).
d) The height, H, over which the density falls off by a factor of 1/e, \[H=\frac{kT}{mg}\]where m is the mean mass of a gas particle, is called the scale height. When astronomers talk about the "thickness" of an atmosphere, we typically mean the scale height of the atmosphere. While formally the solution is defined even when r goes to infinity, atmospheres with greater scale height are "puffier" than those with smaller scale height. What should happen when you increase/decrease m, T, and g?
Looking at the units of H, we can tell that it's actually a height: \([H]=\frac{[dyne\times cm/K][K]}{[g][cm/s^2}=cm\), since \(dyne=\frac{erg}{cm}=\frac{g\times cm}{s^2}\).
This equation indicates that at higher temperatures, the atmosphere should be "puffier." This makes sense, since at higher temperatures the atmospheric gas will expand. With greater values of m (average particle mass) or g, the atmosphere will have a lower scale height. This makes sense, because heavier particles or stronger gravity will result in gas that stays closer to the planet.
e) What is the Earth's scale height, \(H_\oplus\)? The mass of a proton is \(1.7\times10^{-24}g\), and the Earth's atmosphere is mostly molecular nitrogen, N2. Take the average temperature for Earth's atmosphere to be ~250K.
\(H_\oplus=\frac{(1.4\times10^{-16}erg/K)(250K)}{28\times1.7\times10^{-24}g)(980cm/s^2)}=7.5\times10^5cm=7.5km\)
Week 5: Astrophysics in a Nutshell Ch3.1-3.4
This section of Astrophysics in a Nutshell covered the Virial theorem and radiative energy transport in stars. Something that I thought was interesting from this chapter was the idea of mean free path and random walk of photons within a star. The mean free path is the average distance that a photon can travel without getting absorbed and reemitted by a different particle. This distance is inversely dependent on the density of material through which the proton is traveling, so a photon traveling through something really dense, like the interior of a star, will have a smaller mean free path than a photon traveling through empty space.
When the photon gets reemitted, it gets reemitted in a direction independent of its original direction. As a result, the photon doesn't travel in a straight line. Instead, its movement is described as a random walk.
Sources:
Astrophysics in a Nutshell, Dan Moaz
http://stream1.gifsoup.com/webroot/animatedgifs7/2863395_o.gif
https://en.wikipedia.org/wiki/Random_walk
https://en.wikipedia.org/wiki/Quantum_Cloud
http://www2.ess.ucla.edu/~jewitt/images/random.gif
https://en.wikipedia.org/wiki/Milky_Way#Size_and_mass
https://en.wikipedia.org/wiki/Sun
When the photon gets reemitted, it gets reemitted in a direction independent of its original direction. As a result, the photon doesn't travel in a straight line. Instead, its movement is described as a random walk.
 |
| ..not this kind of random walk. |
A random walk is essentially just a series of random steps. I knew a bit about random walks in a biology context, but it turns out that the concept is really useful in fields ranging from economics, physics, computer science, and even art.
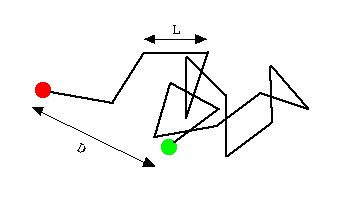
As the photon travels through the star's interior, it's constantly getting absorbed and reemitted such that its path looks less like a straight line and more like the path below:
Obviously, moving at a constant speed, it takes longer to travel the random walk path than it would to just move from the green point to the red point. The density of the Sun is so great and the random walk is so pronounced that a photon produced in the center of the Sun--even moving at the speed of light--would take over 50,000 years to travel to the surface of the Sun. That's an average speed of about 1% of 1 mph! Once released from the Sun, over the next 50,000 years, that photon will have traveled across half of our galaxy--that is, unless it gets absorbed by something else in its path along the way.
Sources:
Astrophysics in a Nutshell, Dan Moaz
http://stream1.gifsoup.com/webroot/animatedgifs7/2863395_o.gif
https://en.wikipedia.org/wiki/Random_walk
https://en.wikipedia.org/wiki/Quantum_Cloud
http://www2.ess.ucla.edu/~jewitt/images/random.gif
https://en.wikipedia.org/wiki/Milky_Way#Size_and_mass
https://en.wikipedia.org/wiki/Sun
Friday, February 26, 2016
Week 5: I can see my house from here!
Sort of.
This is a shot of part of the United States' east coast, taken from the International Space Station. Recently featured on Astronomy Picture of the Day, it captures six major cities: Norfolk on the far left, followed by Richmond, Washington, D.C., Baltimore, Philadelphia, and finally New York City on the far right. Also included in this shot (but somehow inexplicably not worth mentioning in the photo's APOD description) is my hometown of some 6,000 people, located somewhere more or less between the bright patches of D.C. and Baltimore.
While the photos that are taken of objects in space are really amazing (see: pretty much every other photo on APOD), it's also pretty cool what we can see just by pointing a camera at our own planet--especially when that camera is pointed from hundreds of miles above Earth. Satellite images aren't just pretty pictures, either--they can actually be useful. Google uses satellite imagery to power Google Maps, for example, and satellite images are really important for weather reporting.
Sources:
http://apod.nasa.gov/apod/image/1602/NorthEastUSA_ISS_4256.jpg
https://en.wikipedia.org/wiki/International_Space_Station
https://en.wikipedia.org/wiki/Google_Earth
https://en.wikipedia.org/wiki/Satellite_imagery
http://giphy.com/gifs/cat-lol-news-Vr6ZgLp3kYWT6
https://i.ytimg.com/vi/ogtKe7N05F0/maxresdefault.jpg
https://i.ytimg.com/vi/ogtKe7N05F0/maxresdefault.jpg
http://www.airspacemag.com/photos/top-nasa-photos-of-all-time-9777715/
This is a shot of part of the United States' east coast, taken from the International Space Station. Recently featured on Astronomy Picture of the Day, it captures six major cities: Norfolk on the far left, followed by Richmond, Washington, D.C., Baltimore, Philadelphia, and finally New York City on the far right. Also included in this shot (but somehow inexplicably not worth mentioning in the photo's APOD description) is my hometown of some 6,000 people, located somewhere more or less between the bright patches of D.C. and Baltimore.
While the photos that are taken of objects in space are really amazing (see: pretty much every other photo on APOD), it's also pretty cool what we can see just by pointing a camera at our own planet--especially when that camera is pointed from hundreds of miles above Earth. Satellite images aren't just pretty pictures, either--they can actually be useful. Google uses satellite imagery to power Google Maps, for example, and satellite images are really important for weather reporting.
...but not they're not the most important things for weather reporting.
|
On top of that, satellite photos can reveal a whole new perspective of our planet, and can open our eyes to things we hadn't considered before. Before I saw a satellite image of the Northern lights, I thought that they were just an optical illusion of some sort that were dependent on a terrestrial vantage point. After seeing pictures like the one below, I realized that the lights aren't an illusion, and I became interested in learning more about what they were.
Finally, satellite images can inspire. There's not much cooler than a picture of an astronaut with the Earth (and on it almost every other person in existence) looming in the background. Doesn't it make you feel like we can do anything?
 |
| This is another image taken from the ISS. |
 |
| The first untethered space walk (1984). |
Sources:
http://apod.nasa.gov/apod/image/1602/NorthEastUSA_ISS_4256.jpg
https://en.wikipedia.org/wiki/International_Space_Station
https://en.wikipedia.org/wiki/Google_Earth
https://en.wikipedia.org/wiki/Satellite_imagery
http://giphy.com/gifs/cat-lol-news-Vr6ZgLp3kYWT6
https://i.ytimg.com/vi/ogtKe7N05F0/maxresdefault.jpg
https://i.ytimg.com/vi/ogtKe7N05F0/maxresdefault.jpg
http://www.airspacemag.com/photos/top-nasa-photos-of-all-time-9777715/
Monday, February 22, 2016
Week 4: Anatomy of the Sun
As (most) people know, the Sun is a star. Since it's relatively very close to us, it's the most well-studied star by far. In fact, our class is studying the Sun (specifically its size, rotational speed, and period) in our lab this semester. It's about 8 light-minutes from the Earth, has a mass over 300,000 times that of the Earth, and a surface temperature around 5,800K. However, the Sun is more than just a ginormous blob of plasma--we wouldn't be around without the Sun, so let's try to show some respect. Instead, the Sun actually has a fairly well-defined structure:
Like the Earth, the Sun has a core. Like the Earth, the Sun's core is hotter than its surface. Unlike the Earth, the Sun's core is about 15 million degrees Kelvin. Most of the heat of the Sun comes from the core, which extends to about 25% of the solar radius (this gives it about 30 times the radius of the Earth, for comparison). This heat is produced by the fusion of hydrogen nuclei into helium nuclei, which releases a small amount of energy for each reaction, but these reactions add up--almost 1039 of these reactions occur each second.
The next layer is the radiative zone, in which energy is transferred via radiation. It takes a long time for radiation to pass through this layer--gamma rays take over 170,000 years to make the trip from the core to the Sun's next layer. This is because any radiation that is emitted is quickly absorbed and re-emitted by the particles in this region, so there's no way of taking anything remotely resembling a direct path out of the core.
Next is the convection zone, where convection is the main form of energy transport. The convection zone and the radiative zone rotate slightly differently from one another, resulting in a dividing layer between the two known as the tachocline. This allows hot plasma to rise away from the Sun's center and cool ("cool" being ~5800K) plasma to sink back towards the core, thus creating currents and transporting heat and energy towards the surface.
Finally, the surface of the Sun--known as the photosphere--is where energy can finally be released into space and towards everyone trying to get a tan here on Earth. Interestingly, the photosphere, which is mostly composed of atomic hydrogen, is actually more transparent than the air on Earth. The surface and atmosphere of the Sun have their own features. These include the heliosphere, which is full of solar wind, and the corona, which for unknown reasons can reach temperatures up to 20 million Kelvin--a number that definitely puts my complaints about 80˚F temperatures in the summer in perspective.
Sources
https://en.wikipedia.org/wiki/Sun
https://ase.tufts.edu/cosmos/pictures/stars/Fig5_5Anatomy_of_the_Sun.jpg
https://en.wikipedia.org/wiki/Earth
https://en.wikipedia.org/wiki/Radiation_zone
https://en.wikipedia.org/wiki/Convection_zone
https://imgs.xkcd.com/comics/the_sun.png
Like the Earth, the Sun has a core. Like the Earth, the Sun's core is hotter than its surface. Unlike the Earth, the Sun's core is about 15 million degrees Kelvin. Most of the heat of the Sun comes from the core, which extends to about 25% of the solar radius (this gives it about 30 times the radius of the Earth, for comparison). This heat is produced by the fusion of hydrogen nuclei into helium nuclei, which releases a small amount of energy for each reaction, but these reactions add up--almost 1039 of these reactions occur each second.
The next layer is the radiative zone, in which energy is transferred via radiation. It takes a long time for radiation to pass through this layer--gamma rays take over 170,000 years to make the trip from the core to the Sun's next layer. This is because any radiation that is emitted is quickly absorbed and re-emitted by the particles in this region, so there's no way of taking anything remotely resembling a direct path out of the core.
Next is the convection zone, where convection is the main form of energy transport. The convection zone and the radiative zone rotate slightly differently from one another, resulting in a dividing layer between the two known as the tachocline. This allows hot plasma to rise away from the Sun's center and cool ("cool" being ~5800K) plasma to sink back towards the core, thus creating currents and transporting heat and energy towards the surface.
Finally, the surface of the Sun--known as the photosphere--is where energy can finally be released into space and towards everyone trying to get a tan here on Earth. Interestingly, the photosphere, which is mostly composed of atomic hydrogen, is actually more transparent than the air on Earth. The surface and atmosphere of the Sun have their own features. These include the heliosphere, which is full of solar wind, and the corona, which for unknown reasons can reach temperatures up to 20 million Kelvin--a number that definitely puts my complaints about 80˚F temperatures in the summer in perspective.
Sources
https://en.wikipedia.org/wiki/Sun
https://ase.tufts.edu/cosmos/pictures/stars/Fig5_5Anatomy_of_the_Sun.jpg
https://en.wikipedia.org/wiki/Earth
https://en.wikipedia.org/wiki/Radiation_zone
https://en.wikipedia.org/wiki/Convection_zone
https://imgs.xkcd.com/comics/the_sun.png
Week 4: Black Holes
I recently read a brief article about one of the largest known supermassive black holes, located within an elliptical galaxy called NGC 4889. The black hole at the center of this galaxy has a mass about 21 billion times the mass of the Sun--as a point of comparison, the black hole at the center of the Milky Way, Sagittarius A*, is 5000 times smaller, weighing in at "only" 4 million times the Sun's mass. As I was looking over the article, I encountered some black hole terminology that I was mostly familiar with, but wanted to find out a bit more about, so this post is an attempt to better understand black holes (at least qualitatively).
Supermassive black hole: These are the largest type of black hole, generally found at the center of galaxies. While our own black hole is considered supermassive, there are clearly a lot of black holes that are even more massive. Andromeda's, for example, is around 25-50 times more massive than Sagittarius A*, despite the fact that Andromeda and the Milky Way are fairly close in mass. Interestingly, larger black holes tend to have lower densities than smaller black holes, meaning that the forces at the event horizon of a supermassive black hole are actually less than those at the event horizon of a smaller black hole.
Event horizon: While the event horizon has a more technical quantum mechanical definition having to do with the passage of information, it's essentially the point at which a black hole's gravity is so strong that not even light can escape. This boundary is defined by the black hole's mass, with more massive black holes having larger event horizons. The volume enclosed within the event horizon is actually what's used to calculate the density of black holes, which is part of the reason why more massive black holes are considered less dense. While event horizons are important in physics, I think Douglas Adams' application of the event horizon in The Restaurant at the End of the Universe may be even more important:
Sources
http://www.iflscience.com/hubble-takes-new-look-gigantic-black-hole-and-its-quiet-host
https://en.wikipedia.org/wiki/Supermassive_black_hole
https://en.wikipedia.org/wiki/Andromeda_Galaxy
https://en.wikipedia.org/wiki/Milky_Way
https://telescoper.wordpress.com/2010/07/16/the-shoe-event-horizon/
The Restaurant at the End of the Universe, Douglas Adams
https://en.wikipedia.org/wiki/Accretion_disk
Supermassive black hole: These are the largest type of black hole, generally found at the center of galaxies. While our own black hole is considered supermassive, there are clearly a lot of black holes that are even more massive. Andromeda's, for example, is around 25-50 times more massive than Sagittarius A*, despite the fact that Andromeda and the Milky Way are fairly close in mass. Interestingly, larger black holes tend to have lower densities than smaller black holes, meaning that the forces at the event horizon of a supermassive black hole are actually less than those at the event horizon of a smaller black hole.
Event horizon: While the event horizon has a more technical quantum mechanical definition having to do with the passage of information, it's essentially the point at which a black hole's gravity is so strong that not even light can escape. This boundary is defined by the black hole's mass, with more massive black holes having larger event horizons. The volume enclosed within the event horizon is actually what's used to calculate the density of black holes, which is part of the reason why more massive black holes are considered less dense. While event horizons are important in physics, I think Douglas Adams' application of the event horizon in The Restaurant at the End of the Universe may be even more important:
Many years ago this was a thriving, happy planet – people, cities, shops, a normal world. Except that on the high streets of these cities there were slightly more shoe shops than one might have thought necessary. And slowly, insidiously, the number of the shoe shops were increasing. It’s a well-known economic phenomenon but tragic to see it in operation, for the more shoe shops there were, the more shoes they had to make and the worse and more unwearable they became. And the worse they were to wear, the more people had to buy to keep themselves shod, and the more the shops proliferated, until the whole economy of the place passed what I believe is termed the Shoe Event Horizon, and it became no longer economically possible to build anything other than shoe shops. Result – collapse, ruin and famine.
Accretion disk: An accretion disk is formed when diffuse material spirals around a star, black hole, or other massive object. The gravitational force on the material causes it to increase in temperature, compress, and emit electromagnetic radiation. The frequency of the radiation that's emitted from an accretion disk can help astronomers determine what type of body is at the center of the disk. Final fun fact: the study of accretion disks is called discoseismology, which, I would imagine, was the dream job of many an astronomer in the 70s.
 |
| Honestly I thought this search would give me more to work with. |
Sources
http://www.iflscience.com/hubble-takes-new-look-gigantic-black-hole-and-its-quiet-host
https://en.wikipedia.org/wiki/Supermassive_black_hole
https://en.wikipedia.org/wiki/Andromeda_Galaxy
https://en.wikipedia.org/wiki/Milky_Way
https://telescoper.wordpress.com/2010/07/16/the-shoe-event-horizon/
The Restaurant at the End of the Universe, Douglas Adams
https://en.wikipedia.org/wiki/Accretion_disk
Saturday, February 20, 2016
Week 4: WS8 #1
1. The matter between stars is known as the interstellar medium and is composed of mostly dust and gas. This dust absorbs stellar light and therefore reduces the apparent brightness of stars as viewed from the Earth. This effect is known as extinction and worsens as we observe more distant stars.
a) Using trigonometric parallax you measure that the distance to a particular star is 200pc. You know that the absolute magnitude of this star should be 2 and measure an apparent magnitude of 12. How much flux have you lost due to the intervening dust?
We know the equation relating magnitudes and distances is \(M=m-5[log(d)-1]\), so we can just plug in what we know to calculate what the apparent magnitude should have been.
\(2=m-5[log(200)-1]\)
m = 8.5, so ∆m = 3.5.
b) Optical depth is a measure of the absorption of photons as they travel through a medium. The definition of optical depth is \[\tau=ln(I_{in}/I_{out})\]where I denotes the specific intensity of the source. In this problem, we are looking at a single source at a fixed distance, so we can also express \(\tau\) in terms of the flux: \[\tau=ln(F_{in}/F_{out})\]Use this latter definition to determine the relationship between \(\tau\) and the apparent magnitude. What is the optical depth along the line of sight to the star in the previous problem?
We can plug the equation relating flux and magnitude (\(\frac{F_1}{F_2}=10^{0.4(m_2-m_1)}\), where \(m_1\) and \(m_2\) correspond to \(m_{in}\) and \(m_{out}\) respectively) into the equation for \(\tau\):
\(\tau=ln[10^{0.4(m_{out}-m_{in})}]\)
\(\tau=ln[10^{0.4(3.5)}]\approx3.2\)
c) We can now compute the amount of dust required along our line of sight to produce the observed extinction. The optical depth along a line of sight can be calculated from the absorption cross section of any intervening material and the number density of the particles within that cross section. This can be written \[\tau=N\times\sigma\]where N is the total number of particles per cm2 in the line of sight and \(\sigma\) is the cross section of the individual particles.
Assume that each dust grain has the typical size of \(r=0.1\mu m\) and is spherical. Calculate the geometric cross section of a dust grain in units of cm2. Assume that this geometric cross section is the absorption cross section, which is true for visible light. Determine how many particles per cm2 you would need to obtain the calculated optical depth. This value is referred to as a "column number density."
\(\sigma=\pi r^2=\pi(0.1\times10^{-4})^2=3.14\times10^{-10}cm^2\)
\(N=\frac{\tau}{\sigma}=\frac{3.2}{3.14\times10^{-10}cm^2}\approx1\times10^{10}particles/cm^2\)
d) We know that the mass in gas is about 100 times more than in dust. What is the column number density of gas along the same line of sight?
Since we want to find the number density of gas, we can say \(m_{dust}N_{dust}(100)=m_{gas}N_{gas}\).
We know \(N_{dust}=10^{10}particles/cm^2\).
We can estimate the density \(\rho_{dust}=2.2g/cm^3\) and thus calculate \(m_{dust}=(2.2)(4/3)(\pi)(0.1\times10^{-4})^3=9.2\times10^{-15}g\).
Finally we can estimate the mass of gas by assuming that each gas molecule has the mass of hydrogen gas: \(m_{gas}=3.3\times10^{-24}g\).
\(N_{gas}=\frac{m_{dust}N_{dust}100}{m_{gas}}\approx2.8\times10^{21}/cm^2\)
e) What is the average gas density along the same line of sight? Express your answer as the number of particles per cm3.
We simply have to divide the column number density by the distance to the star (200pc, or \(6.2\times10^{20}cm\)), which gives us approximately 4.5 gas molecules per cm3.
a) Using trigonometric parallax you measure that the distance to a particular star is 200pc. You know that the absolute magnitude of this star should be 2 and measure an apparent magnitude of 12. How much flux have you lost due to the intervening dust?
We know the equation relating magnitudes and distances is \(M=m-5[log(d)-1]\), so we can just plug in what we know to calculate what the apparent magnitude should have been.
\(2=m-5[log(200)-1]\)
m = 8.5, so ∆m = 3.5.
b) Optical depth is a measure of the absorption of photons as they travel through a medium. The definition of optical depth is \[\tau=ln(I_{in}/I_{out})\]where I denotes the specific intensity of the source. In this problem, we are looking at a single source at a fixed distance, so we can also express \(\tau\) in terms of the flux: \[\tau=ln(F_{in}/F_{out})\]Use this latter definition to determine the relationship between \(\tau\) and the apparent magnitude. What is the optical depth along the line of sight to the star in the previous problem?
We can plug the equation relating flux and magnitude (\(\frac{F_1}{F_2}=10^{0.4(m_2-m_1)}\), where \(m_1\) and \(m_2\) correspond to \(m_{in}\) and \(m_{out}\) respectively) into the equation for \(\tau\):
\(\tau=ln[10^{0.4(m_{out}-m_{in})}]\)
\(\tau=ln[10^{0.4(3.5)}]\approx3.2\)
c) We can now compute the amount of dust required along our line of sight to produce the observed extinction. The optical depth along a line of sight can be calculated from the absorption cross section of any intervening material and the number density of the particles within that cross section. This can be written \[\tau=N\times\sigma\]where N is the total number of particles per cm2 in the line of sight and \(\sigma\) is the cross section of the individual particles.
Assume that each dust grain has the typical size of \(r=0.1\mu m\) and is spherical. Calculate the geometric cross section of a dust grain in units of cm2. Assume that this geometric cross section is the absorption cross section, which is true for visible light. Determine how many particles per cm2 you would need to obtain the calculated optical depth. This value is referred to as a "column number density."
\(\sigma=\pi r^2=\pi(0.1\times10^{-4})^2=3.14\times10^{-10}cm^2\)
\(N=\frac{\tau}{\sigma}=\frac{3.2}{3.14\times10^{-10}cm^2}\approx1\times10^{10}particles/cm^2\)
d) We know that the mass in gas is about 100 times more than in dust. What is the column number density of gas along the same line of sight?
Since we want to find the number density of gas, we can say \(m_{dust}N_{dust}(100)=m_{gas}N_{gas}\).
We know \(N_{dust}=10^{10}particles/cm^2\).
We can estimate the density \(\rho_{dust}=2.2g/cm^3\) and thus calculate \(m_{dust}=(2.2)(4/3)(\pi)(0.1\times10^{-4})^3=9.2\times10^{-15}g\).
Finally we can estimate the mass of gas by assuming that each gas molecule has the mass of hydrogen gas: \(m_{gas}=3.3\times10^{-24}g\).
\(N_{gas}=\frac{m_{dust}N_{dust}100}{m_{gas}}\approx2.8\times10^{21}/cm^2\)
e) What is the average gas density along the same line of sight? Express your answer as the number of particles per cm3.
We simply have to divide the column number density by the distance to the star (200pc, or \(6.2\times10^{20}cm\)), which gives us approximately 4.5 gas molecules per cm3.
Friday, February 19, 2016
Week 4: WS7 #3
3. One of the most common ways to measure the distance to a star is using the "trigonometric parallax." This works by measuring the angular distance a star appears to move, with respect to a background field of much more distant stars, as the Earth moves one quarter of an orbit (i.e. as the Earth translates "sideways" by a distance b = 1AU).
There are 60 arcminutes in a degree and 60 arcseconds in an arcminute. What is the distance, measured in cm and light years, of a star that moves by 1 arcsecond when the Earth moves by 1AU? Give a general formula relating distance d to the angle \(\theta\), moved by the star.
First we can convert the angle to radians.
\(1"\frac{1'}{60"}\frac{1^\circ}{60'}\frac{\pi}{180}=4.8\times10^{-6}\)
This is a really small angle, so we can use the small angle approximation to say that the distance from the star to the Sun is the same as the distance from the star to the Earth.
There are 60 arcminutes in a degree and 60 arcseconds in an arcminute. What is the distance, measured in cm and light years, of a star that moves by 1 arcsecond when the Earth moves by 1AU? Give a general formula relating distance d to the angle \(\theta\), moved by the star.
First we can convert the angle to radians.
\(1"\frac{1'}{60"}\frac{1^\circ}{60'}\frac{\pi}{180}=4.8\times10^{-6}\)
This is a really small angle, so we can use the small angle approximation to say that the distance from the star to the Sun is the same as the distance from the star to the Earth.
This also allows us to say that \(tan\theta=\theta\).
\(tan\theta=\theta=\frac{1AU}{d}\)
Plugging in \(\theta\) and solving for d, we get \(d=3.13\times10^{18}cm=3.29ly\). This makes sense, because these are approximately the values of a parsec--a unit that's defined as 1AU/1".
Week 4: Astrophysics in a Nusthell Chapter 2.3
Chapter 2.3 of Astrophysics in a Nutshell details the Hertzsprung-Russell diagram, which is used to classify and understand stars. The H-R diagram is a plot of luminosity vs. surface temperature:
 |
| Annoyingly, temperature is conventionally shown to decrease to the right. |
Stars can be classified into three main groups: the main sequence, red giants, and white dwarfs. The main sequence, which is the diagonal line in the middle of the diagram, is where most stars spend the majority of their time. Our Sun lies on the main sequence, along with stars with radii anywhere from 1/4 to 25 that of the Sun. Initially it was believed that stars moved along the main sequence from hot to cool as they aged, but we've learned that that's not the case. Instead, old stars tend to become red giants.
 |
| A rare photo of a cluster of 7 red giants. |
Red giants are larger, redder, and more luminous than stars on the main sequence, so they form their own cluster above the main sequence line. They continue to die, shrinking in size and increasing in temperature as they lose their outer layers, finally becoming white dwarf stars. Since white dwarfs are less luminous than the main sequence stars, they lie below the main sequence on the H-R diagram. Eventually, these stars will radiate away all of their energy and become a theorized type of star called a black dwarf.
If the dying star is really massive, though, it might explode as it collapses under its own gravity. The resulting supernova will create either a black hole or a neutron star--extremely dense stars with very little luminosity. Neutron stars can pack 1-3 times the mass of the Sun into a sphere of radius 7 miles. That means that over 17,000 neutron stars could fit between the Earth and the Moon, or that I could drive past two neutron stars going from my home to my high school. It probably wouldn't be great for the commute, but I guess it'd be better than having red giants (or slow drivers) in the way.
Sources
Astrophysics in a Nutshell, Dan Moaz
https://upload.wikimedia.org/wikipedia/commons/1/17/Hertzsprung-Russel_StarData.png
http://cdn11.ne.be/movies/10527/31736.jpg
https://en.wikipedia.org/wiki/Black_dwarf
https://en.wikipedia.org/wiki/Neutron_star
Monday, February 15, 2016
Week 3: Astrophysics in a Nutshell Chapter 2.1
This chapter of Astrophysics in a Nutshell was essentially a super condensed version of problem 2 that I worked through a couple posts ago (maybe I'll start doing the readings before trying to struggle through the worksheets...). While reading over simplified versions of the derivations that I already spent a couple hours on today was certainly no less than scintillating, the most interesting sentence in the chapter for me was during the discussion of Wien's law (reminder that Wien's law defines the relation between the temperature of a blackbody--such as a star--with its peak emitted wavelength): "In fact, the eyesight of most animals on Earth apparently evolved to have the most sensitivity in the wavelength range within which the Sun emits the most energy."
This is a really cool idea (no, seriously)! First of all, it makes total sense now that I know about it, but it isn't something that I would've come up with on my own. The fact that the Sun's peak wavelength is located in the center of the visual spectrum is what gave rise to the *visible* spectrum in the first place. Had the Sun been a different temperature, the \(\lambda_{max}\) would be completely different too, and our eyes would have probably evolved differently. The visible spectrum in that case would be a completely different range of wavelengths.
This is interesting when thinking about planets that orbit stars of temperatures different from that of our Sun. In the off-chance that complex life has developed on such a planet, they would probably see things completely differently than we do. While this idea is pretty awesome in general (especially from a biology standpoint), I think the coolest ramification is that maybe, somewhere, there are aliens that just naturally have x-ray vision--who knows?*
*Given the wavelengths of x-rays (0.01-10nm) and Wien's law, pretty much no stars are hot enough (a minimum of 290000K) for their peak wavelengths to be in the x-ray range, so never mind. :(
Sources
Astrophysics in a Nutshell, Dan Maoz
http://www.theopticalvisionsite.com/wp-content/uploads/2013/09/X-ray-man.jpg
https://en.wikipedia.org/wiki/X-ray
https://upload.wikimedia.org/wikipedia/commons/6/6b/HRDiagram.png
This is a really cool idea (no, seriously)! First of all, it makes total sense now that I know about it, but it isn't something that I would've come up with on my own. The fact that the Sun's peak wavelength is located in the center of the visual spectrum is what gave rise to the *visible* spectrum in the first place. Had the Sun been a different temperature, the \(\lambda_{max}\) would be completely different too, and our eyes would have probably evolved differently. The visible spectrum in that case would be a completely different range of wavelengths.
This is interesting when thinking about planets that orbit stars of temperatures different from that of our Sun. In the off-chance that complex life has developed on such a planet, they would probably see things completely differently than we do. While this idea is pretty awesome in general (especially from a biology standpoint), I think the coolest ramification is that maybe, somewhere, there are aliens that just naturally have x-ray vision--who knows?*
 |
| They almost definitely use glasses like this to see visible light. |
*Given the wavelengths of x-rays (0.01-10nm) and Wien's law, pretty much no stars are hot enough (a minimum of 290000K) for their peak wavelengths to be in the x-ray range, so never mind. :(
Sources
Astrophysics in a Nutshell, Dan Maoz
http://www.theopticalvisionsite.com/wp-content/uploads/2013/09/X-ray-man.jpg
https://en.wikipedia.org/wiki/X-ray
https://upload.wikimedia.org/wikipedia/commons/6/6b/HRDiagram.png
Week 3: Cassiopeia
For Valentine's Day, since my roommate and I were both Valentine-less, we decided to watch a chick flick on Netflix to distract us from our own lonely lives. The film was actually pretty bad, but the constellation Cassiopeia featured briefly. I vaguely knew of the constellation beforehand (I think I got to see it this summer), but the movie piqued my interest (in part because I hadn't thought of anything else to write this post about).
As can be seen above, the constellation is composed of 5 stars in a W-shape. Supposedly this shape depicts the Aethiopian queen Cassiopeia, who was mother to Andromeda and was imprisoned in the sky for bragging that her daughter was more beautiful than the sea nymphs. I don't really see it, and honestly, I've never been sure how the Greeks came up with this stuff--I'm just going to assume it's because they didn't have much else to do besides philosophizing and stargazing back in those days.
The four brightest stars that form the constellation range from about 50 to about 550 light years away from the Earth. Although it's obvious in hindsight, I hadn't considered that stars in a constellation could be much farther from each other than they are from us--I guess it can still be pretty easy to fall victim to the ancient idea that the sky is basically a giant sphere surrounding the Earth. The brightest of the stars, Alpha Cassiopeia, is over 600 times more luminous than the Sun and has a mass approximately 5 times that of the Sun.
There are also several other objects located within the constellation. M52 and M103 are open clusters (small groups of clustered stars created from the same giant molecular cloud) that are located within Casseopeia. These are much farther than the stars in the constellation--both are over 5000 light years from the Earth. Finally, two supernovae have been observed in the region of Cassiopeia. One of these was even farther than the clusters--10,000 or so light years away. Thinking about the widely varying distances in just this one constellation makes me wonder what sort of crazy stories the Greeks could've come up with if Earth were in a different part of the Milky Way and had a completely different perspective.
Sources
https://en.wikipedia.org/wiki/Cassiopeia_(constellation)
https://upload.wikimedia.org/wikipedia/commons/c/c1/CassiopeiaCC.jpg
https://en.wikipedia.org/wiki/Alpha_Cassiopeiae
https://en.wikipedia.org/wiki/Open_cluster
Week 3: WS6 #2
2. Consider the amount of energy produced by the Sun per unit time, also known as the bolometric luminosity, \(L_{\odot}\). That same amount of energy per time is present at the surface of all spheres centered on the sun at distances r > \(R_{\odot}\). However, the flux at a given patch on the surface of these spheres depends on r.
a) How does flux, F, depend on luminosity, L, and distance, r?
Since the luminosity remains constant, the flux must decrease as the light spreads out from the Sun in a sphere (essentially the photons are spreading out as they move away from the Sun). The relation, then, is just the luminosity divided by the surface area of the expanding sphere: \(F=\frac{L}{4\pi r^2}\)
b) The Solar flux at the Earth-Sun distance has been measured to high precision, and for the purposes of this exercise is given by \(F_{\oplus}=1.4\times10^6\frac{ergs}{cm^2s}\). Given that the Sun's angular diameter is \(\theta=0.57^{\circ}\), what is the effective temperature of the Sun?
Since the luminosity remains constant, we can set the luminosities at the two distances equal. This means:
\(4\pi R_{\odot}^2F_{\odot}=4\pi a^2F_{\oplus}\), where \(R_{\odot}\) is the radius of the Sun and a is 1AU, or the distance from the Earth to the Sun (\(1.5\times10^{13}cm\)).
\(R_{\odot}^2F_{\odot}=a^2F_{\oplus}\)
\(F_{\odot}=\frac{a^2F_{\oplus}}{R_{\odot}^2}\)
Now that we've figured out what the flux at the surface of the Sun should be, we can use that to find the temperature using \(F=\sigma T^4\), where \(\sigma=5.7\times 10^{-5}\frac{erg}{cm^2sK^4}\), the Stefan-Boltzmann constant.
\(T=(\frac{F_{\odot}}{\sigma})^{1/4}\)
\(T=(\frac{a^2F_\oplus}{R_\odot^2\sigma})^{1/4}\)
We have a and \(F_\oplus\), but we need to find \(R_\odot\). We can do this based on the angular diameter of the Sun, using trig:
a) How does flux, F, depend on luminosity, L, and distance, r?
Since the luminosity remains constant, the flux must decrease as the light spreads out from the Sun in a sphere (essentially the photons are spreading out as they move away from the Sun). The relation, then, is just the luminosity divided by the surface area of the expanding sphere: \(F=\frac{L}{4\pi r^2}\)
b) The Solar flux at the Earth-Sun distance has been measured to high precision, and for the purposes of this exercise is given by \(F_{\oplus}=1.4\times10^6\frac{ergs}{cm^2s}\). Given that the Sun's angular diameter is \(\theta=0.57^{\circ}\), what is the effective temperature of the Sun?
Since the luminosity remains constant, we can set the luminosities at the two distances equal. This means:
\(4\pi R_{\odot}^2F_{\odot}=4\pi a^2F_{\oplus}\), where \(R_{\odot}\) is the radius of the Sun and a is 1AU, or the distance from the Earth to the Sun (\(1.5\times10^{13}cm\)).
\(R_{\odot}^2F_{\odot}=a^2F_{\oplus}\)
\(F_{\odot}=\frac{a^2F_{\oplus}}{R_{\odot}^2}\)
Now that we've figured out what the flux at the surface of the Sun should be, we can use that to find the temperature using \(F=\sigma T^4\), where \(\sigma=5.7\times 10^{-5}\frac{erg}{cm^2sK^4}\), the Stefan-Boltzmann constant.
\(T=(\frac{F_{\odot}}{\sigma})^{1/4}\)
\(T=(\frac{a^2F_\oplus}{R_\odot^2\sigma})^{1/4}\)
We have a and \(F_\oplus\), but we need to find \(R_\odot\). We can do this based on the angular diameter of the Sun, using trig:
\(R_\odot=7.46\times10^{10}cm\)
Finally, we can plug all the values in and solve to get a final answer \(T\approx5600K\).
Week 3: WS5 #2
2. a) In astronomy, it is often useful to deal with something called the "bolometric flux," or the energy per area per time, independent of frequency. Integrate the blackbody flux \(F_\nu(T)\) over all frequencies to obtain the bolometric flux emitted from a blackbody, F(T).
We were given that \(F_\nu(T)=\frac{4\pi\nu^2}{c^2}\frac{h\nu}{e^{h\nu/kT}-1}\), which we then have to integrate.
\(\frac{4\pi}{c^2}\int^\infty_0\frac{h\nu^3}{e^{h\nu/kT}-1}d\nu\)
We define \(u=h\nu/kT\).
\(\frac{4\pi}{c^2}\int^\infty_0\frac{h(ukT/h)^3}{e^u-1}(kT/h)du\)
\(\frac{4\pi k^4T^4}{c^2h^3}\int^\infty_0\frac{u^3}{e^u-1}du\)
The integral is defined as \(\frac{\pi^4}{15}\), so we can pull that out and define \(\frac{4\pi^5k^4}{15c^2h^3}=\sigma\) (a constant).
The final equation is \(F(T)=\sigma T^4\)
b) The Wein Displacement Law: Convert the units of the blackbody intensity from \(B_\nu(T)\) to \(B_\lambda(T)\).
The relation between the blackbody intensity in terms of frequency and the intensity in terms of wavelength is defined such that the integral of the two equations are equal.
\(\int^\infty_0B_\nu d\nu=\int^0_\infty B_\lambda d\lambda=-\int^\infty_0B_\lambda d\lambda\)
We can get rid of the integral such that \(B_\nu d\nu=-B_\lambda d\lambda\).
Since we know that \(B_\nu(T)=\frac{2\nu^2}{c^2}\frac{h\nu}{e^{h\nu/kT}-1}\) and that \(\nu=\frac{c}{\lambda}\) (and therefore that \(d\nu=\frac{-c}{\lambda^2}d\lambda\)), we can simply plug in the values to do this conversion.
\(B_\lambda(T)d\lambda=\frac{-2(c/\lambda)^2}{c^2}\frac{h(c/\lambda)}{e^{hc/\lambda kT}-1}\frac{-c}{\lambda^2}d\lambda\)
\(B_\lambda(T)d\lambda=\frac{2}{\lambda^5}\frac{hc^2}{e^{hc/\lambda kT}-1}d\lambda\)
We can cancel out \(d\lambda\) to get the final answer:
\(B_\lambda(T)=\frac{2}{\lambda^5}\frac{hc^2}{e^{hc/\lambda kT}-1}\)
c) Derive an expression for the wavelength \(\lambda_{max}\) corresponding to the peak of the intensity distribution at a given temperature T.
In order to do this, we want to take the partial derivative in terms of wavelength of the equation we derived in part (b) and set it equal to zero to find the maximum wavelength.
\(\frac{\partial}{\partial\lambda}[\frac{2}{\lambda^5}\frac{hc^2}{e^{hc/\lambda kT}-1}]\)
By u-substitution (\(u=\frac{hc}{\lambda kT}\)), we can condense this expression:
\(\frac{\partial}{\partial u}[\frac{2}{(hc/\lambda kT)^5}\frac{hc^2}{e^u-1}]\)
After a bunch of calculus, we have found the derivative and can set it to zero.
\(\frac{2(kT)^5(hc^2)}{(hc)^5}\frac{(e^u-1)(5u^4)-(e^u)(u^5)}{(e^u-1)^2}=0\)
Solving this equation gives us \(5=\frac{ue^u}{e^u-1}\).
If we assume that u is very large, we can simplify to \(5=\frac{ue^u}{e^u}\) yielding the final result that \(u=\frac{hc}{\lambda kT}\approx5\). Solving for \(\lambda_{max}\) and plugging in the constants, we end with the equation \(\lambda_{max}=\frac{0.283}{T}\).
d) The Rayleigh-Jeans Tail: Next, let's consider photon energies that are much smaller than the thermal energy. Use a first-order Taylor expansion on the term \(e^{h\nu/kT}\) to derive a simplified form of \(B_\nu(T)\) in this low-energy regime.
If we assume that \(\frac{h\nu}{kT}\) is very small, we can assume that \(e^{h\nu/kT}\approx1+\frac{h\nu}{kT}\).
\(B_\nu(T)=\frac{2}{c^2}\frac{h\nu^3}{e{h\nu/kT}-1}\)
\(B_\nu(T)=\frac{2}{c^2}\frac{h\nu^3}{1+\frac{h\nu}{kT}-1}\)
\(B_\nu(T)=\frac{2\nu^2kT}{c^2}\)
e) Write an expression for the total power output of a blackbody with radius R, starting with the expression for \(F_\nu\). This total energy output per unit time is also known as the bolometric luminosity, L.
We've already figured out that \(F(T)=\sigma T^4\). Since the luminosity is simply all of the flux over the entire surface area of the sphere of expanding radiation, we can simply multiply the flux by the surface area of a sphere to yield \(L=\sigma T^44\pi R^2\).
We were given that \(F_\nu(T)=\frac{4\pi\nu^2}{c^2}\frac{h\nu}{e^{h\nu/kT}-1}\), which we then have to integrate.
\(\frac{4\pi}{c^2}\int^\infty_0\frac{h\nu^3}{e^{h\nu/kT}-1}d\nu\)
We define \(u=h\nu/kT\).
\(\frac{4\pi}{c^2}\int^\infty_0\frac{h(ukT/h)^3}{e^u-1}(kT/h)du\)
\(\frac{4\pi k^4T^4}{c^2h^3}\int^\infty_0\frac{u^3}{e^u-1}du\)
The integral is defined as \(\frac{\pi^4}{15}\), so we can pull that out and define \(\frac{4\pi^5k^4}{15c^2h^3}=\sigma\) (a constant).
The final equation is \(F(T)=\sigma T^4\)
b) The Wein Displacement Law: Convert the units of the blackbody intensity from \(B_\nu(T)\) to \(B_\lambda(T)\).
The relation between the blackbody intensity in terms of frequency and the intensity in terms of wavelength is defined such that the integral of the two equations are equal.
\(\int^\infty_0B_\nu d\nu=\int^0_\infty B_\lambda d\lambda=-\int^\infty_0B_\lambda d\lambda\)
We can get rid of the integral such that \(B_\nu d\nu=-B_\lambda d\lambda\).
Since we know that \(B_\nu(T)=\frac{2\nu^2}{c^2}\frac{h\nu}{e^{h\nu/kT}-1}\) and that \(\nu=\frac{c}{\lambda}\) (and therefore that \(d\nu=\frac{-c}{\lambda^2}d\lambda\)), we can simply plug in the values to do this conversion.
\(B_\lambda(T)d\lambda=\frac{-2(c/\lambda)^2}{c^2}\frac{h(c/\lambda)}{e^{hc/\lambda kT}-1}\frac{-c}{\lambda^2}d\lambda\)
\(B_\lambda(T)d\lambda=\frac{2}{\lambda^5}\frac{hc^2}{e^{hc/\lambda kT}-1}d\lambda\)
We can cancel out \(d\lambda\) to get the final answer:
\(B_\lambda(T)=\frac{2}{\lambda^5}\frac{hc^2}{e^{hc/\lambda kT}-1}\)
c) Derive an expression for the wavelength \(\lambda_{max}\) corresponding to the peak of the intensity distribution at a given temperature T.
In order to do this, we want to take the partial derivative in terms of wavelength of the equation we derived in part (b) and set it equal to zero to find the maximum wavelength.
\(\frac{\partial}{\partial\lambda}[\frac{2}{\lambda^5}\frac{hc^2}{e^{hc/\lambda kT}-1}]\)
By u-substitution (\(u=\frac{hc}{\lambda kT}\)), we can condense this expression:
\(\frac{\partial}{\partial u}[\frac{2}{(hc/\lambda kT)^5}\frac{hc^2}{e^u-1}]\)
After a bunch of calculus, we have found the derivative and can set it to zero.
\(\frac{2(kT)^5(hc^2)}{(hc)^5}\frac{(e^u-1)(5u^4)-(e^u)(u^5)}{(e^u-1)^2}=0\)
Solving this equation gives us \(5=\frac{ue^u}{e^u-1}\).
If we assume that u is very large, we can simplify to \(5=\frac{ue^u}{e^u}\) yielding the final result that \(u=\frac{hc}{\lambda kT}\approx5\). Solving for \(\lambda_{max}\) and plugging in the constants, we end with the equation \(\lambda_{max}=\frac{0.283}{T}\).
d) The Rayleigh-Jeans Tail: Next, let's consider photon energies that are much smaller than the thermal energy. Use a first-order Taylor expansion on the term \(e^{h\nu/kT}\) to derive a simplified form of \(B_\nu(T)\) in this low-energy regime.
If we assume that \(\frac{h\nu}{kT}\) is very small, we can assume that \(e^{h\nu/kT}\approx1+\frac{h\nu}{kT}\).
\(B_\nu(T)=\frac{2}{c^2}\frac{h\nu^3}{e{h\nu/kT}-1}\)
\(B_\nu(T)=\frac{2}{c^2}\frac{h\nu^3}{1+\frac{h\nu}{kT}-1}\)
\(B_\nu(T)=\frac{2\nu^2kT}{c^2}\)
e) Write an expression for the total power output of a blackbody with radius R, starting with the expression for \(F_\nu\). This total energy output per unit time is also known as the bolometric luminosity, L.
We've already figured out that \(F(T)=\sigma T^4\). Since the luminosity is simply all of the flux over the entire surface area of the sphere of expanding radiation, we can simply multiply the flux by the surface area of a sphere to yield \(L=\sigma T^44\pi R^2\).
Friday, February 12, 2016
Week 3: Gravitational waves
Yesterday, a breakthrough was announced in astrophysics: the first detection of gravitational waves. Gravitational waves were initially predicted by Einstein's theory of general relativity, but they hadn't been detected until September 2015. Their detection provides strong support for general relativity, as well as providing an avenue for studying the universe that is fundamentally different from just using electromagnetic radiation. I think this is probably the aspect of this discovery that I am most excited about--just last week I was wondering what telescopes would be like if they functioned less like the human eye, and using gravity as an observational tool could play that role. (Was I in on the discovery? Was it just coincidence? The mystery continues...)
Essentially what happened was that two black holes, one 36 times and one 29 times the mass of the Sun, collided and released 3 times the Sun's mass in pure energy. Remember, \(E=mc^2\) (another shout-out to Einstein), so this is a lot of energy--50 times the power of everything else in the visible universe, in fact. This energy was released largely in the form of gravitational waves, which is why LIGO (Laser Interferometer Gravitational Wave Observatory) was able to detect them, even though the event occurred 1.3 billion light years away (and therefore 1.3 billion years ago). The video below is a visualization of the two black holes orbiting each other and finally colliding. This video is in fact in slow motion--the actual event happened in just tenths of a second, with the black holes reaching half the speed of light in their orbit.
While this has been the most impressive signal received so far, there were a couple of smaller signals received during the 5 month detecting period. This is pretty cool because it means that the technology is working and that events are happening in the universe that are within our threshold of detection. It'll be really exciting to see how this can be used to advance our understanding of gravity, general relativity, and the universe as a whole.
Sources
https://www.ligo.caltech.edu/video/ligo20160211v3
http://gizmodo.com/physicists-are-freaking-out-about-gravitational-waves-a-1758605484
http://www.nytimes.com/2016/02/12/science/ligo-gravitational-waves-black-holes-einstein.html?_r=0
https://en.wikipedia.org/wiki/General_relativity#Gravitational_wave_astronomy
http://apod.nasa.gov/apod/ap160212.html
Essentially what happened was that two black holes, one 36 times and one 29 times the mass of the Sun, collided and released 3 times the Sun's mass in pure energy. Remember, \(E=mc^2\) (another shout-out to Einstein), so this is a lot of energy--50 times the power of everything else in the visible universe, in fact. This energy was released largely in the form of gravitational waves, which is why LIGO (Laser Interferometer Gravitational Wave Observatory) was able to detect them, even though the event occurred 1.3 billion light years away (and therefore 1.3 billion years ago). The video below is a visualization of the two black holes orbiting each other and finally colliding. This video is in fact in slow motion--the actual event happened in just tenths of a second, with the black holes reaching half the speed of light in their orbit.
While this has been the most impressive signal received so far, there were a couple of smaller signals received during the 5 month detecting period. This is pretty cool because it means that the technology is working and that events are happening in the universe that are within our threshold of detection. It'll be really exciting to see how this can be used to advance our understanding of gravity, general relativity, and the universe as a whole.
Sources
https://www.ligo.caltech.edu/video/ligo20160211v3
http://gizmodo.com/physicists-are-freaking-out-about-gravitational-waves-a-1758605484
http://www.nytimes.com/2016/02/12/science/ligo-gravitational-waves-black-holes-einstein.html?_r=0
https://en.wikipedia.org/wiki/General_relativity#Gravitational_wave_astronomy
http://apod.nasa.gov/apod/ap160212.html
Monday, February 8, 2016
Week 2: Astrophysics in a Nutshell Chapter 1
Chapter 1 of Astrophysics in a Nutshell essentially focused on how telescopes worked, but the most interesting part for me was the parallels drawn between telescopes and the human eye (again, I'm much more a biologist than a physicist). Like telescopes, the human eye has a both a "camera" and a "detector"--the lens in the front of the eye focuses the light onto the retina in the back of the eye in the same way telescopes may use mirrors to focus light onto a CCD or other type of detector.
Many vision problems arise from misalignments of the focused light in the eye, and for centuries, concave and convex lenses have been used as vision correctors. On top of that, people have been staring at the sky for pretty much as long as people have been around to look at anything. It's not surprising, then, that in some ways the human eye served as inspiration for telescopes, and that the first telescopes used lenses to magnify the light.
Sources
https://en.wikipedia.org/wiki/History_of_the_telescope
http://www.antiquetelescopes.org/history.html
https://cnx.org/resources/465ef69789306dc609b2650a92697be3e852a6e7/Figure_27_01_02.jpg
http://www.easyeyes.com/images/pedsc.jpg
Many vision problems arise from misalignments of the focused light in the eye, and for centuries, concave and convex lenses have been used as vision correctors. On top of that, people have been staring at the sky for pretty much as long as people have been around to look at anything. It's not surprising, then, that in some ways the human eye served as inspiration for telescopes, and that the first telescopes used lenses to magnify the light.
 |
| The lens focuses light onto the retina, although the image is flipped--a problem which is corrected by the brain. |
However, telescopes soon surpassed eyes in almost every regard (which would be sad if it weren't kind of the point of telescopes in the first place). First of all, modern telescopes can increase their integration time. This allows for the detection of a larger number of photons, which strengthens the signal of faint sources. Our eye has a very short, fixed integration time of only a fraction of a second, which isn't conducive to astronomy, but also prevents us from being blinded by the Sun, so it's probably a net positive. Our eyes are also pretty small, which again isn't conducive to gathering tons of photons. If you've ever had your eyes dilated, that increases the pupil size, allowing more photons to enter. This is why the ophthalmologist's office always gives you those super cheap sunglasses after every appointment.
 |
| Swag. |
You never see telescopes wearing those cool glasses though, because it's to an astronomer's advantage to gather as many photons as possible, and this is facilitated by having a larger area over which to gather photons. Finally, the eye is limited in that it can only detect electromagnetic radiation in the visible spectrum (hence the name "visible spectrum"). Telescopes, on the other hand, can be set to detect wavelengths in different parts of the spectrum. This is helpful since a lot of astronomy occurs outside of the visible light range, so we'd never be able to be able to detect all that information without them, even if our eyes were otherwise comparable to telescopes.
One interesting thing to think about is whether there are alternative forms that telescopes could take that are less based on the human eye, and what the advantages and disadvantages of something like that would be.
Sources
https://en.wikipedia.org/wiki/History_of_the_telescope
http://www.antiquetelescopes.org/history.html
https://cnx.org/resources/465ef69789306dc609b2650a92697be3e852a6e7/Figure_27_01_02.jpg
http://www.easyeyes.com/images/pedsc.jpg
Week 2: WS4 #2
2. CCAT is a 25-meter telescope that will detect light with wavelengths up to 850 microns. How does the angular resolution of this huge telescope compare to the angular resolution of the much smaller MMT 6.5-meter telescope observing in the infrared J-band?
We determined in a previous problem that the resolution \(\theta\) is equal to \(\frac{\lambda}{D}\), where \(\lambda\) is the wavelength of the light observed and D is the diameter of the telescope. If we say the J-band is 1.2 microns, we can simply calculate and compare the resolutions.
\(\theta_{CCAT}=\frac{850\times10^{-6}m}{25m}=3.4\times10^{-5}\)
\(\theta_{MMT}=\frac{1.2\times10^{-6}m}{6.5m}=1.8\times10^{-7}\)
Since smaller resolution is better, we know that MMT has the better resolution.
Corrected 2/14/16
Sources
https://en.wikipedia.org/wiki/J_band
We determined in a previous problem that the resolution \(\theta\) is equal to \(\frac{\lambda}{D}\), where \(\lambda\) is the wavelength of the light observed and D is the diameter of the telescope. If we say the J-band is 1.2 microns, we can simply calculate and compare the resolutions.
\(\theta_{CCAT}=\frac{850\times10^{-6}m}{25m}=3.4\times10^{-5}\)
\(\theta_{MMT}=\frac{1.2\times10^{-6}m}{6.5m}=1.8\times10^{-7}\)
Since smaller resolution is better, we know that MMT has the better resolution.
Corrected 2/14/16
Sources
https://en.wikipedia.org/wiki/J_band
Sunday, February 7, 2016
Week 2: WS3 #2
2. The Local Sidereal Time (LST) is the right ascension that is at the meridian right now. LST = 0:00 is at noon on the Vernal Equinox (the time when the Sun is on the meridian March 20th, for 2013 and 2014).
a) What is the LST at midnight on the Vernal Equinox?
Sidereal time is based on the time it takes for the Earth to complete exactly one rotation, rather than how long it takes for the same for the same point to realign with the Sun. As a result of the Earth's rotation around the Sun, these times differ slightly--LST picks up 4 minutes per day over "regular" time. Therefore, at midnight (12 hours after noon) on the Vernal Equinox, the LST would be 12:02.
b) What is the LST 24 hours later (after midnight in part 'a')?
An extra 24 hours would mean an extra 4 minutes; 12:06.
c) What is the LST right now (to the nearest hour)?
During our class time (2:30-4pm) on Tuesday, February 2, we calculated that the LST would be approximately 1:00--1 month and 18 days before the Vernal Equinox translates to a loss of about 3 hours. At 4pm, this would make the LST about 1:00.
d) What will the LST be tonight at midnight (to the nearest hour)?
Approximately 8 hours after class time would make the LST about 9:00.
e) What LST will it be at sunset on your birthday?
My birthday is July 27. If sunset is at 8pm, that makes this 4 months, 7 days, and 8 hours after noon on March 20th. This translates to a gain of 8:29 and an LST of 16:29.
a) What is the LST at midnight on the Vernal Equinox?
Sidereal time is based on the time it takes for the Earth to complete exactly one rotation, rather than how long it takes for the same for the same point to realign with the Sun. As a result of the Earth's rotation around the Sun, these times differ slightly--LST picks up 4 minutes per day over "regular" time. Therefore, at midnight (12 hours after noon) on the Vernal Equinox, the LST would be 12:02.
b) What is the LST 24 hours later (after midnight in part 'a')?
An extra 24 hours would mean an extra 4 minutes; 12:06.
c) What is the LST right now (to the nearest hour)?
During our class time (2:30-4pm) on Tuesday, February 2, we calculated that the LST would be approximately 1:00--1 month and 18 days before the Vernal Equinox translates to a loss of about 3 hours. At 4pm, this would make the LST about 1:00.
d) What will the LST be tonight at midnight (to the nearest hour)?
Approximately 8 hours after class time would make the LST about 9:00.
e) What LST will it be at sunset on your birthday?
My birthday is July 27. If sunset is at 8pm, that makes this 4 months, 7 days, and 8 hours after noon on March 20th. This translates to a gain of 8:29 and an LST of 16:29.
Week 2: The Pillars of Creation
"Pillars of Creation" is one of my favorite photographs of all time--in fact, it's actually my desktop background, which hopefully contributes to my astro street cred without being too nerdy. First of all, its colors and form are beautiful. The picture was taken in both visible and infrared spectra, which allows the capture of the densest regions of the structure. The glow around the pillars (which might be my favorite part of the picture) is the vaporization of the material on the periphery. Unfortunately, this means that this incredible structure is gradually disappearing.
Second, this thing is huge--the pillar on the left is about four light years long. It's composed of molecular hydrogen and is an active star forming region. Thinking about the sheer size and the vast amount of hydrogen, the lightest element, that must be present to form structures as large and dense as stars is mind-boggling. In fact, the stars that this thing has created provide a large part of the energy that is destroying the pillars. Kind of sad, isn't it?
A final interesting fact about this photo is that it was taken in 2014 as kind of a tribute to a famous picture taken by the Hubble telescope in 1995--an awesome image in its own right:
Sources
http://www.astronomy.com/-/media/Images/News%20and%20Observing/News/2015/01/Pillars2014.jpg?mw=600
https://en.wikipedia.org/wiki/Pillars_of_Creation
https://upload.wikimedia.org/wikipedia/commons/b/b2/Eagle_nebula_pillars.jpg
Thursday, February 4, 2016
Week 2: Planet X
As probably everyone who is remotely interested in astronomy has heard, a new planet was recently discovered. What's notable about this planet is that it orbits our own Sun, which makes it a candidate for inclusion in The Official Planet Roster Of Our Solar System--a list from which Pluto was crossed off in 2006.
While Planet X (whose name for some reason just reminds me of Chemical X from the Powerpuff Girls) has been detected due to its gravitational effects on other objects in our solar system, including the minor planet Sedna, it hasn't been visually detected. Part of the reason for this is because of how far away it is. Estimates for its closest approach are around 200 AU--almost 7 times that of Neptune, the most distal planet in our solar system (since Pluto's demotion at least)--and its farthest distance could be as large as 1,200 AU. At that distance, it would take light from the Sun almost a week to reach the planet. This makes it pretty difficult to find with a telescope.
In an ironic twist, one of the scientists who published results supporting the existence of Planet X was Mike Brown, a Caltech scientist whose previous work directly led to Pluto's demotion. On discovering Planet X, he said, "Killing Pluto was fun, but this is head and shoulders above everything else." Harsh.
Sources:
https://www.centralmaine.com/2016/01/27/the-discovery-of-planet-x/
http://ih0.redbubble.net/image.77569687.6291/raf,220x200,075,f,black.u5.jpg
https://en.wikipedia.org/wiki/Pluto
https://en.wikipedia.org/wiki/90377_Sedna
http://www.sciencemag.org/news/2016/01/feature-astronomers-say-neptune-sized-planet-lurks-unseen-solar-system
https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEim9temp3WPCmNNxpr03SbtAAKjeBqRM6ZpyowVuvYbQtxMNYOsXCcvExzwsHez5aPwTM_fhOsjAQ1ntIIVV9SgRLKBPnRRfmYVF6P7_FzefLwGhGpxMVaImToYCHMhl6sUErQ3MsEfNv81/s1600/sad+pluto4.jpg
While Planet X (whose name for some reason just reminds me of Chemical X from the Powerpuff Girls) has been detected due to its gravitational effects on other objects in our solar system, including the minor planet Sedna, it hasn't been visually detected. Part of the reason for this is because of how far away it is. Estimates for its closest approach are around 200 AU--almost 7 times that of Neptune, the most distal planet in our solar system (since Pluto's demotion at least)--and its farthest distance could be as large as 1,200 AU. At that distance, it would take light from the Sun almost a week to reach the planet. This makes it pretty difficult to find with a telescope.
In an ironic twist, one of the scientists who published results supporting the existence of Planet X was Mike Brown, a Caltech scientist whose previous work directly led to Pluto's demotion. On discovering Planet X, he said, "Killing Pluto was fun, but this is head and shoulders above everything else." Harsh.
Sources:
https://www.centralmaine.com/2016/01/27/the-discovery-of-planet-x/
http://ih0.redbubble.net/image.77569687.6291/raf,220x200,075,f,black.u5.jpg
https://en.wikipedia.org/wiki/Pluto
https://en.wikipedia.org/wiki/90377_Sedna
http://www.sciencemag.org/news/2016/01/feature-astronomers-say-neptune-sized-planet-lurks-unseen-solar-system
https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEim9temp3WPCmNNxpr03SbtAAKjeBqRM6ZpyowVuvYbQtxMNYOsXCcvExzwsHez5aPwTM_fhOsjAQ1ntIIVV9SgRLKBPnRRfmYVF6P7_FzefLwGhGpxMVaImToYCHMhl6sUErQ3MsEfNv81/s1600/sad+pluto4.jpg
Subscribe to:
Comments (Atom)