Week 8: WS14 #3

3. For the transit light curve and radial velocity time series, and assuming a 3.1 day orbit, 

a) What is the qualitative brightness distribution of the star's surface as viewed from the Earth? 

Normally, these plots are straight at the bottom, rather than curved. This plot indicates that the star in question is brighter in the center than at the edges, which means that the transiting planet makes the most difference when it's directly in front of the planet.

b) What is the planet's radius compared to the star's radius? 

When the planet is directly in front of the star, it cuts off on average about 2.7% of the star's light, based on the light curve. This should relate directly to their radii:
\(0.027=\frac{A_p}{A_\star}=\frac{\pi R_p^2}{\pi R_\star^2}\)
\(\frac{R_p}{R_\star}=0.164\)

c) What is the planet's semimajor axis compared to the star's radius? 

On a previous problem we determined that \(t_{transit}=\frac{2R_\star P}{2\pi a}\). It appears that the transit time (the time it takes for the planet's center to traverse the star) takes 180 minutes, or 10800 seconds. We know that the period is 3.1 days or 267840 seconds.
\(10800s=\frac{R_\star(267840s)}{\pi a}\)
\(\frac{a}{R_\star}=7.89\)

d) What is the size of the planet compared to Jupiter if the star has a radius of \(0.8R_\odot\)? 

\(\frac{R_p}{R_\star}=\frac{R_p}{0.8R_\odot}=0.164\)
\(R_p=\frac{0.1312R_\odot}{1}\frac{1R_{Jup}}{0.1R_\odot}=1.312R_{Jup}\)

e) Show that the scaled semimajor axis, \(a/R_\star\), is related to the stellar density. 

We can solve Kepler's third law for stellar mass:
\(P^2=\frac{4\pi^2a^3}{GM_\star}\)
\(M_\star=\frac{4\pi^2a^3}{GP^2}\)
Dividing both sides by the stellar volume will give you the density on the left:
\(\frac{M_\star}{(4/3)\pi R_\star^3}=\frac{4pi^2a^3}{GP^2}\frac{3}{4\pi R_\star^3}\)
\(\rho_\star=\frac{3\pi}{GP^2}(\frac{a}{R_\star})^3\)

f) What is the density of the star compared to the density of the Sun? 

\(\rho_\star=\frac{3\pi}{6.674\times10^{-8}cm^3/gs^2)(267840s)^2}(7.89)^3=0.968g/cm^3\)
This is smaller than the Sun's density, 1.408g/cm.

g) What is the density of the planet compared to the density of Jupiter? 

In a previous worksheet we determined the relation between the star's speed K and its mass, the planet's mass, and the period:
\(m_p=K(\frac{PM_\star^2}{2\pi G})^{1/3}\)
However, we need to find the mass of the star first. Since we know the density of the star and its size compared to the Sun, we can calculate its mass:
\(\frac{\rho_\star}{\rho_\odot}=\frac{0.968}{1.408}=\frac{(M_\star/R_\star^3)}{(M_\odot/R_\odot^3)}\)
\(0.687\frac{M_\odot}{R_\odot^3}=\frac{M_\star}{R_\star^3}\)
\(0.687\frac{M_\odot}{M_\star}=\frac{R_\odot^3}{R_\star^3}=(\frac{1}{0.8})^3\)
\(0.3517M_\odot=M_\star\)
\(M_\star\approx7\times10^{32}g\)
Now we can calculate the planet's mass:
\(m_p=(50000cm/s)(\frac{(267840s)(7\times10^{32}g)^2}{2\pi(6.674\times10^{-8}cm^3/gs^2)})^{1/3}=3.39\times10^{30}g\)
Now we can find the ratio between the planet's density and Jupiter's density:
\(\frac{\rho_p}{\rho_{Jup}}=\frac{\frac{3.39\times10^{30}g}{(4/3)\pi(1.312R_{Jup})^3}}{\frac{1.90\times10^{30}g}{(4/3)\pi(R_{Jup})^3}}=\frac{3.39\times10^{30}}{(1.90\times10^{30})(2.26)}=0.79\)
This planet is about 79% the density of Jupiter.

Week 8: WS13 #1

1. a) We often say that planets orbit stars. But planets and their stars actually orbit their mutual center of mass, which in general is given by \(x_{com}=\sum_im_ix_i\sum_im_i\). Set up the problem by drawing an x-axis with the star at \(x=-a_\star\) with mass \(M_\star\), and the planet at \(x=a_p\) and \(m_p\). Also, set \(x_{com}=0\). How do \(a_p\) and \(a_\star\) depend on the masses of the star and planet? 

Since we know that  \(x_{com}=\sum_im_ix_i\sum_im_i\), we can say that \(x_{com}=\frac{-a_\star M_\star+a_pm_p}{M_\star+m_p}\). Setting \(x_{com}=0\) allows us to determine that \(M_\star a_\star=m_pa_p\). 

b) In a two-body orbital system the variable a is the mean semimajor axis, or the sum of the planet's and star's distances away from their mutual center of mass: \(a=a_p+a_\star\). Label this on your diagram. Now derive the relationship between the total mass \(M_\star+m_p\approx M_\star\), orbital period P, and the mean semimajor axis a, starting with the Virial Theorem for a two-body orbit. 

The Virial Theorem states that \(-\frac{1}{2}U=K\) or \(-\frac{1}{2}\frac{GMm}{r}=\frac{1}{2}mv^2\). Since the planet is much smaller than the star, the center of mass will be much closer to the star and therefore \(a\approx a_p\). This allows us to find the velocity based on the planet's period: \(v=\frac{2\pi a}{P}\).

\(m_p(\frac{2\pi a}{P})^2=\frac{GM_\star m_p}{a}\)

\(\frac{4\pi a^2}{P^2}=\frac{GM}{a}\)

\(P^2=\frac{4\pi^2a^3}{GM}\) 

This is Kepler's third law! 

c) By how much is the Sun displaced from the Solar System's center of mass as a result of Jupiter's orbit? Express this displacement in a useful unit such as Solar radii. (Potentially useful numbers: \(M_\odot\approx1000M_{Jup}\) and \(a_{jup}\approx5.2AU\).)

\(M_\star a_\star=m_pa_p\)
\(1000M_{Jup}a_\odot=M_{Jup}5.2AU\)
\(a_\odot=0.0052AU\)
\(\frac{0.0052AU}{1}\frac{1.5\times10^8km}{1AU}\frac{1R_\odot}{7.0\times10^5km}\approx1R_\odot\): Jupiter displaces the Sun by about one Solar radius.

Week 8: The Hercules-Corona Borealis Great Wall

One of the largest objects ever observed is called the Hercules-Corona Borealis Great Wall. While the name alone is impressive, it pales in comparison to the object itself. The HCBGW is essentially a region that is more densely populated than average with galaxy clusters and other matter. This structure is approximately 10 billion light years across. Since this is so large, it's helpful to think about it in different terms: this structure is about 10% the size of the observable universe, and spans a third of our sky, despite being about 10 billion light years away from us. In cgs units, this object is hella big.

The HCBGW. The bright clumps indicate dark matter. Zooming in recommended.

The first indication of this object's existence was the detection of an unexpectedly large number of gamma ray bursts coming from the region. Gamma ray bursts generally indicate the presence of matter, and upon further analysis, scientists concluded that it was extremely likely that the bursts were coming from the same aggregation of matter. This whole process, as far as I can tell, is pretty routine for observational astronomers. What wasn't routine was how large the HCBWG turned out to be. 

I think the most interesting thing about the size of the HCBWG is the implication that it has towards our understandings of cosmology. The cosmological principle is the idea that the universe is uniform and the same in every direction, when viewed on a large enough scale. Basically, this idea is a more formal way of saying that no location in the universe is "special." Since we want to avoid inhomogeneities that don't disappear when you've zoomed out enough, there must be an upper limit on the size that any one astronomical object can attain. This theoretical limit was set on the order of hundreds of megaparsecs. 

The HCBWG, if it can truly be considered one object, however, is about 3000 megaparsecs, blowing this limit out of the water. Critics of the cosmological principle have cited the HCBWG and other almost-comparably-gigantic objects such as the Huge Large Quasar Group (not to be confused with any large huge quasar groups, apparently) as evidence against the hypothesis. While I have no beef with the cosmological principle, I can't help but hope that the Hercules-Corona Borealis Great Wall truly is one gargantuan object, because it would just be so cool.




Sources
http://listverse.com/2015/10/22/10-of-the-biggest-things-in-the-universe/
https://en.wikipedia.org/wiki/Hercules-Corona_Borealis_Great_Wall
https://upload.wikimedia.org/wikipedia/commons/f/fd/Hubble_image_of_MACS_J0717_with_mass_overlay.jpg
https://en.wikipedia.org/wiki/Cosmological_principle

Week 8: Astrophysics in a Nutshell Ch2.2.4

This section of Astrophysics in a Nutshell covers the different types of binary star systems: visual, astromeric, eclipsing, and spectroscopic binaries. One interesting thing that I learned from this chapter is that it's much easier to determine the masses of stars in binary systems than it is to determine the mass of lone stars--in fact it's essentially impossible for the latter. Estimation of the masses is done using the mass ratio (based on the ratio of the stars' angles) and Kepler's law. An example of a binary star system (while not the most famous) is Sirius A and B. Sirius A, the brightest star we can see at night, has a much fainter white dwarf companion, Sirius B.

After reading this chapter, I was interested in finding out more about binary and multiple star systems. As it turns out, systems with more than two stars are often inherently unstable, as the system's center of gravity is constantly moving. The stars found in systems like this are usually very young, as it doesn't take long for one or more of the stars to be ejected from the system in order to form a more stable system. Here's a screenshot from a simulation of a planet's motion around two stationary stars (although it can easily be thought about as a third smaller star):

Given how complicated and random this motion already appears, it's easy to see that it would be even more unstable if the two suns were moving and exerting gravitational influence on each other as well.

I don't know about you, but I wouldn't want to live in a solar system that looked like this.

We know of star systems with multiplicities up to 7, but in most cases, these systems can be broken down into binary systems with some sort of hierarchy: for example, a binary star system orbiting a third star that's more distant. These orbits are much more stable, since the binary pair can be treated like a single gravitational source, thereby simplifying the system as a whole back down to sort of a pseudo-binary system. Presumably you could figure out the masses of the stars in a system like this using the same kind of calculation as you would for a normal binary system--but in this case, I think the orbits are much more interesting than the masses.

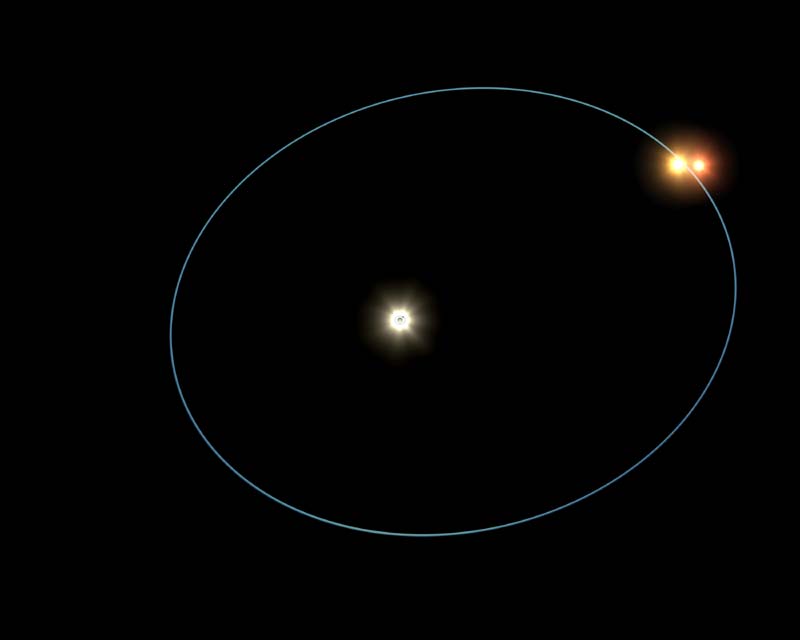The system HD 188753, which is a triple star system

Sources
Astrophysics in a Nusthell, Dan Moaz
https://en.wikipedia.org/wiki/Star_system
http://www.clausewitz.com/mobile/chaosdemos.htm
https://en.wikipedia.org/wiki/HD_188753

Week 8: Earths (and Life) Away From Earth

This week in class we have been talking about how to observe exoplanets. We've learned that in general, larger planets that are closer to their stars, like hot Jupiters, are the easiest to observe. However, for me at least, these aren't the planets that are the most interesting. I'm much more interested in the planets that would be able to support life--especially life as we know it. This is a job that the Kepler Space Telescope has been working on since 2009, and it has found some pretty interesting candidates.

One of the most promising Earth-like planets that Kepler has found is Kepler-186f. This planet, which was discovered in 2014, has a radius about 10-20% larger than that of the Earth. Furthermore, Kepler-186f orbits within a region around its parent star known as the habitable zone. This band is defined as the region in which liquid water can exist, although this definition can be somewhat flexible depending on the mass and atmospheric conditions of the planets in question. Fortunately, Kepler-186f lies in the "conservative" habitable zone, outside of which only larger-than-Earth planets could have liquid water.

While it can be difficult to determine the planet's composition, the planet's small size indicates that it is likely not a gaseous planet. Instead, scientists predict that it is a rocky planet, like our own. Assuming similar composition to Earth's, Kepler-186f would have a mass of about 44% greater than the Earth's (although estimates based on compositions with more water or iron range from a third to about 4 times Earth's mass). However, Kepler-186f is close to 500 lightyears away, which will make investigating its surface for life very difficult until our technology improves.

Searching for life by looking for Earth-like planets that lie in their stars' habitable zones has been criticized by some scientists for focusing too closely on the idea that extraterrestrial life must be carbon-based and need liquid water (an idea which has the awesome name "carbon chauvinism"). For example, silicon, which, like carbon, forms 4 bonds, has been proposed as an alternative basis for biochemical systems, especially for colder environments--which I think this is a really cool idea. However, the only examples of life we know of are all carbon-based, so I think until both observational astronomy and biochemistry have advanced quite a bit, we should stick to what we know.



Sources
http://www.space.com/30172-six-most-earth-like-alien-planets.html
https://en.wikipedia.org/wiki/Kepler-186f
https://en.wikipedia.org/wiki/Circumstellar_habitable_zone
http://www.nasa.gov/ames/kepler/nasas-kepler-discovers-first-earth-size-planet-in-the-habitable-zone-of-another-star
https://en.wikipedia.org/wiki/Carbon_chauvinism
http://topinfopost.com/wp-content/uploads/2015/02/new_earthh.jpg

Week 7: Astrophysics in a Nutshell Ch3.10-3.12

This chapter of Astrophysics in a Nutshell covered the proton-proton chain and how that reaction powers the Sun and other stars. One consequence of the p-p chain that I thought was interesting was the release of neutrinos. This occurs in the first, rate-limiting step of the p-p chain:
\[p+p\rightarrow d+e^++\nu_e.\]The \(\nu_e\) is the neutrino.

Neutrinos are interesting for a lot of reasons. In basic terms, they're very similar to electrons, except they are uncharged (although there are two other types of neutrinos that are more closely related to two other subatomic particles). This means that they're critically different from electrons in that they are not affected by the electromagnetic forces. Because of this, they can travel for vast distances before interacting with any other particles--the mean free path of a neutrino is on the order of 10¹⁸ cm! While this property makes them useful for carrying information from astronomical events vast distances away, it also makes neutrinos very difficult to detect.

One way of detecting neutrinos is by observing its effects on the few particles that it does hit. If a neutrino collides with an atom with high enough energy, the atom will be burst into its constituent protons and neutrons. These particles can be detected by machines such as the Large Hadron Collider. Neutrino collisions with quarks can yield different particles which can also be detected. Regardless of the huge flux of neutrinos from the Sun, we've still detected very few neutrinos, so improvements in our technology will greatly benefit this field.



Sources
Astrophysics in a Nutshell, Dan Moaz
http://www.ps.uci.edu/~superk/neutrino.html
https://icecube.wisc.edu/info/neutrinos
http://profmattstrassler.com/2011/09/25/how-to-detect-neutrinos/

Week 7: WS12.1 #2

2. Let's model a star. Our star will be a ball of gas compressed by its own gravity, held together by gas pressure, and is leaking out energy from its core due to radiative diffusion. 
a) Write down the three equations of stellar structure that we have learned so far: for hydrostatic equilibrium, radiative diffusion, and mass conservation. Supplement this with an equation of state appropriate for matter inside a star. These four equations (plus an equation for energy generation) are the building blocks of our stellar model. 

Mass conservation: \(\frac{dM(r)}{dr}=4\pi r^2\rho(r)\)
Hydrostatic equilibrium: \(\frac{dP}{dr}=\frac{-GM(r)\rho(r)}{r^2}\)
Radiative diffusion: \(\frac{dT(r)}{dr}=\frac{3L(r)\kappa(r)\rho(r)}{16\pi^2acT^3(r)r^2}\)
Equation of state (gas pressure): \(P(r)=nkT=\frac{\rho(r)}{m(r)}kT(r)\)

b) Consider the boundary conditions for the Sun and rewrite the differential equations as proportionalities. 

Mass conservation: \(\frac{\Delta M}{\Delta r}=4\pi r^2\rho(r)\)
If we rearrange this to solve for density, we get \(\rho={M}{4\pi r^3}\), which simplifies to \(\rho\sim\frac{M}{r^3}\). This makes sense based on how we calculate density.

Hydrostatic equilibrium: \(\frac{\Delta P}{\Delta r}=\frac{-GM(r)\rho(r)}{r^2}\)
We can plug in the previously determined proportionality relating density and mass: \(\frac{\Delta P}{\Delta r}=\frac{-GM(r)}{r^2}\frac{M}{r^3}\)
By rearranging, getting rid of the constants, and solving for pressure, we get \(P\sim\frac{M^2}{r^4}\).

Radiative diffusion: \(\frac{\Delta T}{\Delta r}=\frac{3L(r)\kappa(r)\rho(r)}{16\pi^2acT^3(r)r^2}\)
Since opacity and luminosity depend on more than just the radius, we will leave these terms in the proportionality. However, we can substitute in the proportionality for density: \(\frac{\Delta T}{\Delta r}=\frac{3L(r)\kappa(r)}{16\pi^2acT^3(r)r^2}\frac{M}{r^3}\)
This simplifies to the proportionality \(T^4\sim\frac{M\kappa(r)L(r)}{r^4}\).