Week 12: Conclusion

This semester I've learned a lot thanks to Astro 16. In class, we covered topics ranging from sidereal time to the interstellar medium to astrochemistry and astrobiology. We talked about the progression of stars' lives, different strategies for detecting exoplanets, how properties of stars determine stellar structure, and why we wouldn't notice for millennia if the Sun stopped its fusion. I got to use a real telescope, write about recent developments in the field of astronomy, and even draw some connections with evolution and anatomy.

Probably one of the most interesting topics I learned about this semester was planet formation. The planets in our Solar System are pretty diverse in terms of size and composition, but I never knew exactly how they formed or why they're arranged the way they are. It was cool to learn that the mass of the protoplanetary disk material that is needed to form a planet is often much greater than the mass of the "finished" planet. It was also interesting to learn that the temperature and density gradients are a large part of the reason why planets formed the way they did. Hopefully as our understanding of our own Solar System improves, our ability to interpret the planetary systems of other stars will improve correspondingly.

The biggest challenge I've faced in this class (and this was definitely true of Astro 17 last semester as well) has been writing the lab reports. I found lab to be a valuable part of the class, especially as preparation for the Exoplanet Challenge, but I hate writing lab reports. In our first lab, we measured the astronomical unit using the Sun's angular diameter, rotational velocity, and period. Our final calculation was off by a factor of 10...which means there have been better estimates of the Earth-Sun distance since the 1st century BC. I mean, I knew going into the lab that our findings wouldn't exactly be ground-breaking, but I kind of expected that our modern technology would give us a leg up into at least the 14th or 15th century. It doesn't exactly motivate me to do a lab write-up when I know that Ye Olde Lab Reporte would've been way more accurate. As for the second lab report...well, I haven't started, and it's due at the end of the week. So there's that.

Finally, the highlight of the course in my opinion was the astrobiology lecture. Although I've done some reading on my own about astrobiology, I'd love the opportunity to go more in depth on the Drake Equation, the RNA world hypothesis, habitable zones, and anything else that may be necessary to make a planet livable. I honestly wish Harvard offered an entire course or two on astrobio and/or astrochem, because they're such cool subjects and the perfect union of my (admittedly very strange combination of) interests. If I can't find anything here at Harvard, though, maybe the Universe will bring me back to astrobio one day anyway.

Thanks for reading!

Sources 
https://en.wikipedia.org/wiki/Astronomical_unit#History
http://wallpoper.com/images/00/34/00/68/calvin-and_00340068.jpg

Week 11: Live Blogging the Exoplanet Challenge

So tonight from 12:30 am to sunrise, Rodrigo and I are signed up for our first observing session in our quest to complete the Astronomy 16 Exoplanet Challenge. If we successfully observe a transiting exoplanet and write up a brief report on it, we'll automatically get A's in the class. We've chosen to observe HAT-P-37b, an exoplanet with a radius 1.2 times that of Jupiter and a period of 2.8 days, which is supposed to transit its star between 3:04 am and 5:24 am tonight. I'll be live blogging over the course of the night, which should be interesting--both because we'll hopefully be getting some cool data and because my mental faculties will probably be on a sharp decline by around 2:30 am. So here we go!

10:23 pm: Attempt to take a nap. Give up not much later because I only woke up 12 hours ago. Resign myself to being exhausted for the next 24 hours.

11:43 pm: Realize that Dunkin Donuts closes in 17 minutes. Make the sketchy walk from the Quad in the name of caffeine.

11:57 pm: Discover that Dunkin sits on a throne of lies and has closed before midnight. Shake fist and go to Starbucks instead.

12:30 am: Ready to get started! We're taking over the telescope from the group before us, which means that we don't have to worry too much about setup. This would be more handy if the beginning of our transit wasn't still two and a half hours away, but it is nice.

1:57 am: So it took a lot longer than I expected to get things set up, but we just finished up in the dome. Fortunately we're right on schedule--we planned to start taking images right around 2 am so that we'd be prepared when the transit starts around 3. We spent the last hour and a half getting the scope in focus, finding our star, fiddling with the exposure time, and finally setting up the computer to take a bunch of exposures over the next hour or so. Our first few images looked awesome, so I'm optimistic about the rest of the night!

2:45 am: I'm taking advantage of the fact that I haven't collapsed from exhaustion yet to be productive. Maybe this week I'll get all my blog posts done before the hour before they're due! (Sincerest apologies to the lecturers of my bio class, which is right before Astronomy and in which I have finished more than one last-minute blog post...)

2:53 am: *Gets excited all over again about how cool astrochemistry and astrobiology are*

3:13 am: Our first 30 images are done! The transit should have started around 10 minutes ago and it seems like there may have been a decrease in the number of counts on our star, but until we start fooling around with photometry, we won't be able to tell. We were pretty anal following the directions during setup and it's pretty clear out, so I'm really hoping that we can get good data tonight.

3:56 am: It's way past my bedtime.

4:05 am: I just finished the other two blog posts for this week. Now that those are done, I'll be watching some videos to learn how to use some genomic analysis tools for the infectious disease lab I work in. This is peripherally related because the program is called Galaxy, even though all the genomes we have to sequence reside here on Earth. Galaxy is just a cool word I guess.

Thanks for always validating me, Google Images <3

My mentor in lab will be happy that I'm working on this, but probably not happy when I show up 6 hours from now with my eyes taped open. Can't win 'em all, I guess.

4:29 am: Our second set of images is done and we're going to start doing some photometry! Fingers crossed that we like what we see...

5:12 am: Our data doesn't make any sense and now clouds are moving in and I want to go to bed and I haven't even made any progress on Galaxy and I think the last time I stayed up this late was to work on the lab report last semester. This is my life now. *Drowns sorrows in brownies*

5:33 am: So the thing is that we have two decent-looking reference stars with which to compare our star's magnitude (as in their magnitudes remain more or less unchanged in all of our images), but all of the other stars that we've chosen as references seem to follow the same changes in magnitude as our object. I'm pretty sure that the shallow dip that we see in our object's magnitude, since it's matched by the plots of most of the other stars, is not actually legit. At the same time, it doesn't make a lot of sense for two of the reference stars to have normal-looking magnitude profiles if there's something atmospheric or something affecting the brightness of all the other stars.

6:04 am: We just shut the telescope and the computer down and will figure this mess out later. Time to head to Kirkland and crash on my friend's couch until my 8 am meeting!

Epilogue (12:40 pm):

We are true scientists. 

Sources
https://en.wikipedia.org/wiki/List_of_transiting_exoplanets

Week 11: WS20 #1

1. The Earth resides in a "Goldilocks Zone" or habitable zone (HZ) around the Sun. At our semimajor axis we receive just enough sunlight to prevent the planet from freezing over and not too much to boil off our oceans. Not too cold, not too hot. Just right. In this problem we'll calculate how the temperature of a planet, T_p, depends on the properties of the central star and the orbital properties of the planet. 
a) Draw the Sun on the left, and a planet on the right, separated by a distance a. The planet has a radius R_p and temperature T_p. The star has a radius R_★ and a luminosity L_★ and a temperature T_eff. 

b) Due to energy conservation, the amount of energy received per unit time by the planet is equal to the energy emitted isotropically under the assumption that it is a blackbody. How much energy per time does the planet receive from the star? How much energy per time does the planet radiate as a blackbody? 

We know that the flux from the star at the distance a is given by \(F_\bigstar=\frac{L_\bigstar}{4\pi a^2}\). However, this is the total flux, and we want only the power received by the planet. If we multiply the flux by the cross-sectional area of the planet, we get the correct units for power (energy per time) and the proper dependence on the planet's radius.
\(P=\frac{L_\bigstar}{4\pi a^2}(\pi R_p^2)=\frac{L_\bigstar R_p^2}{4a^2}\)
In order to calculate how much energy the planet radiates as a blackbody, we simply use the Stefan-Boltzmann Law to find the flux, and then multiply by the planet's surface area in order to convert to power.
\(F_p=\sigma T_p^4\)
\(P=\sigma T_p^44\pi R_p^2\)

c) Set these two quantities equal to each other and solve for T_p. 

\(\frac{L_\bigstar R_p^2}{4a^2}=\sigma T_p^44\pi R_p^2\)
\(T_p=(\frac{L_\bigstar}{16\pi a^2\sigma})^{1/4}\)

d) How does the temperature change if the planet were much larger or much smaller? 

There's no dependence on the planet's radius in the above equation, so the temperature won't change if the size of the planet changes. This makes sense, because any extra radiation absorbed by the planet due to its increased cross section will be radiated away due to its increased surface area.

e) Not all of the energy incident on the planet will be absorbed. Some fraction, A, will be reflected back out into space. How does this affect the amount of energy received per unit time, and thus how does this affect T_p? 

Any reflected energy will correspond to an equivalent decrease in the energy absorbed by the planet, which will correspond to a decreased surface temperature.

Week 11: WS19 #2

2. Resolving organic chemistry in disks: It is debated whether the Earth's water and organics originated from material forming around 4 AU (asteroid-like) or 30 AU (comet-like). We would therefore like to know what the differences in the organic composition is between these two locations in protoplanetary disks. One of the interesting organics CH₃CN emits strongly at 239 GHz. How big of a telescope would you need to resolve a difference in chemical composition between 4 AU and 30 AU in the nearest star-forming region? How does the required telescope size compare with the biggest steerable radio telescope in operation, the 100 m Green Bank Telescope (GBT)? To the longest baseline in the ALMA interferometer of 10 km? 

First, we should figure out what the wavelength the acetonitrile is emitting at.
\(239GHz=239\times10^9s^{-1}\)
\(\lambda=c/\nu\)
\(\lambda=\frac{3.0\times10^{10}cm/s}{239\times10^9s^{-1}}=0.126cm\)
Let's assume that the nearest star-forming region is 150 parsecs away.

Since we're comparing the signal at 4 AU and 30 AU, the top will be the difference: 26 AU. In order to calculate the angle, we can use the small angle approximation.
\(tan\theta=\frac{26AU}{150pc}=\frac{26AU}{3.09\times10^8AU}\)
\(\theta=\frac{26AU}{3.09\times10^8AU}=8.41\times10^{-8}\)
Finally we can calculate the necessary diameter of the telescope.
\(D=1.22\frac{\lambda}{\theta}\)
\(D=1.22\frac{0.126cm}{8.41\times10^{-8}}=1.83\times10^6cm=18.3km\)
To get the necessary resolution for this, the GBT would be way too small. ALMA is also a bit small, but is the right order of magnitude.

Week 11: The Arecibo Message

On Thursday, our lecture covered astrobiology. While a lot of this field focuses on life as a more general phenomenon, the exciting part of astrobiology for most people is almost definitely the idea of finding intelligent life off of the Earth. However, since the only example of intelligent life that we have is ourselves (and even that can be questionable sometimes), we don't know anything about the culture, capabilities, or even biology of potential life elsewhere in our universe, and it can be difficult to be confident in our definition of intelligent life.

Given our lack of knowledge regarding what we might share with other civilizations, scientists wanted to come up with the most simple and universal way of demonstrating humanity's intelligence. Thus, in 1974, the Arecibo message was born. This message contained what Dr. Frank Drake (of the Drake equation, which we discussed in lecture) and Dr. Carl Sagan deemed the most important information about and known by humans, including the numbers 1-10, the chemical formulas of the nucleotides, Earth's location within our solar system, and the population of Earth. Once the information was assembled, the message was transmitted via an extremely powerful radio broadcast in the direction of a star cluster called M13.

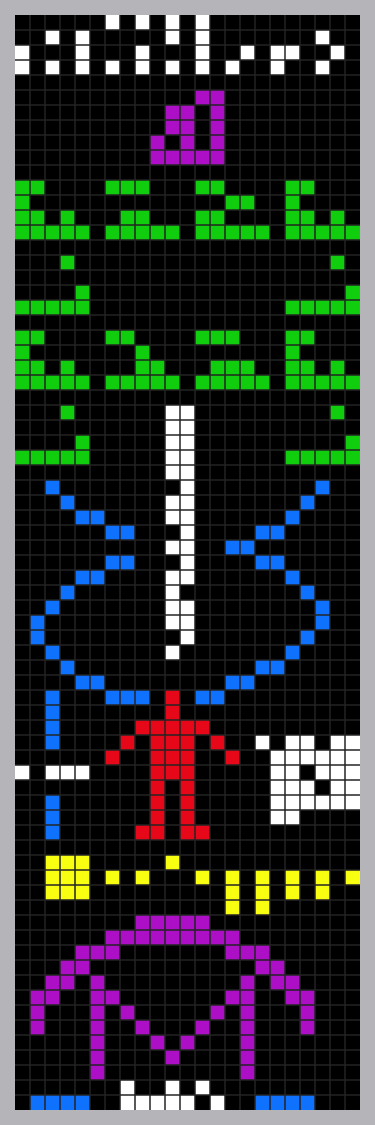A graphic representation of the Arecibo Message. Its dimensions were chosen as 73x23, because prime numbers would lead to minimum confusion when reconstructing the information. 

M13 was chosen because it has a large number of stars, is relatively big, and is relatively close. However, "close" in this case means about 25,000 light years away--which means that it won't be another 24,958 years or so before the Arecibo message reaches M13, and another 25,000 years or so after that before we could possibly get a response. While very little of the information encoded in the message has changed since 1974 (only the Earth's population and the fact that we have demoted Pluto from planethood), a lot can change in 50,000 years--the disappearance of the Neanderthal and all of recorded history are just two small examples of things that have happened in the last 50,000 years, for instance. It's unlikely that the Arecibo Radio Telescope, from which the signal was broadcast and which is represented in the message, will still be around in 50 millennia.

Our understanding of the universe will have changed a lot by then too. Just given how much physics has advanced since 1974 and the accelerating trajectory that that advance has taken, it's possible that at some point before 50,000 years have elapsed, we'll look back on this transmission with embarrassment. "Why did we think it was important to show that we knew how to count to 10? Any respectable civilization would have understood and included the unified field theory instead," we will lament, with the same emotions one feels upon looking at pictures of him- or herself from middle school.

In any case, the Arecibo message is less of an exercise in practical extraterrestrial communication than it is in thinking about what's important and how we can communicate with cultures unimaginably different from ours. That being said, if we haven't made contact with aliens by 51,974, it'll be a suspenseful year for anyone who remembers this transmission.




Sources 
https://en.wikipedia.org/wiki/Arecibo_message
http://phenomena.nationalgeographic.com/files/2014/11/AreciboMessage-e1417162442960.jpg
http://www.seti.org/seti-institute/project/details/arecibo-message
https://en.wikipedia.org/wiki/Messier_13
https://en.wikipedia.org/wiki/Neanderthal
http://outline-of-history.mindvessel.net/80-the-neanderthal-man-an-extinct-race/81-the-world-50000-years-ago.html

Week 10: The Edge of Space

While it has been over 60 years since the first dogs were launched into space by the Russians (clearly the most important part of the space race), recently a group of young students from England managed to do the same...kind of. Using a balloon, they sent a stuffed animal dog named Sam equipped with a GoPro up into space--in the name of science, of course. The video is pretty cool, especially listening to how much quieter things get as Sam increases in altitude. By the end, you can clearly see the Earth's curvature and its atmosphere, and beyond that, the blackness of space.

After I watched this video, I began to wonder exactly where the boundary of space began. There's no clear point where Sam clearly passes from being "in the sky" to "in space," but clearly that transition must happen somewhere. Turns out there are several different definitions that range from about 80 km to about 120 km. NASA, for example, defines the boundary as 122 km based on how vehicles are steered during reentry. Another definition, 100 km, is based on the fact that at this altitude, the velocity needed for atmospheric lift is greater than orbital velocity. A third definition is based on the transition from Earth winds to the winds of charged particles in space.

Unfortunately there's no altimeter included in Sam's journey (or at least not one that appears in the video), so it's hard to tell how many of those barriers he passed. However, it's inspiring to see the English space program making such great leaps forwards.



Sources 
http://www.usatoday.com/videos/news/have-you-seen/2016/04/11/82901316/
https://en.wikipedia.org/wiki/Animals_in_space
https://en.wikipedia.org/wiki/Outer_space

Week 10: Tourism...in Space!

I just read an article describing Bigelow Aerospace's plan to introduce inflatable habitations that could be used in space. The first one will soon be attached to the International Space Station for a two-year-long test, but the company hopes that these units, termed Bigelow Expanding Activity Modules (BEAMs), could eventually exist in space apart from the ISS. This could help ease the demand on the ISS from smaller space programs that don't get as much time on board as programs like NASA do. There is also hope that this will be an important first step towards the commercialization of space. Not only does it have the possibility of initiating space tourism, but it also may give rise to the development of new industries that don't necessarily have to depend on governments.

Leaked photo of actual space tourists. 

This would also be a great way to increase the number of opportunities for scientific research. Not only would there be a wider variety of places to choose from to do microgravity research in fields like biology or medicine, but I think as commercial space programs become more legitimate, on-the-ground research that supplements those programs will become more of a focus as well. We need to take steps forward in the space industry both for their own sake and to keep things moving forward here on Earth.

Finally, I think these habitations would be a really great way of increasing popular support for the space program. Like a true pioneer, Robert Bigelow, the founder of Bigelow Aerospace, really drew attention to what is truly one of the most important goals in the space industry today: "We would love to see Disney have a Disney space station. Wouldn't that be cool?"

It would indeed be cool, Mr. Bigelow.

Sources 
https://www.washingtonpost.com/news/the-switch/wp/2016/04/11/boeing-lockheed-to-launch-habitats-for-space-tourists-and-researchers/
http://graphics8.nytimes.com/images/2011/03/01/science/01orbit/01orbit-articleLarge.jpg
http://vignette4.wikia.nocookie.net/disney/images/4/40/Magic_Kingdom_Space_Mountain_Poster.jpg/revision/latest?cb=20110413013012

Week 10: WS18 #1

1. Hill spheres: One outcome of planet formation is systems of satellites around planets. Now you may ask yourself, why do some planets have moons 100s of millions of kilometers away, while the Earth's moon is only 400,000km away? To answer this question, we need to think about how big of a region around a planet is dominated by the gravity of the planet, i.e. the region where the gravitational pull of the planet is more important than the gravitational pull of the central star (or another planet). 
a) Gravitational forces: Put a test mass somewhere between a star of mass M_s and a planet of mass m_p at a distance r_p from the star. Make a drawing clearly marking these characteristics for the gravitational force on the particle from the star and on the particle from the planet. At what distance r_H from the planet are the two forces balanced? This distance approximates the radius of the Hill sphere, which in the case of planet formation is the sphere of disk material which a planet can accrete from. 

We know that gravitational force is given by \(F_G=\frac{GMm}{r^2}\), so we can just set the gravitational force on the particle from the star and from the planet equal and solve for r_H. 

\(\frac{GM_sm}{(r_p-r_H)^2}=\frac{Gm_pm}{r_H^2}\) 

\(\frac{M_s}{m_p}=(\frac{r_p-r_H}{r_H})^2=(\frac{r_p}{r_H}-1)^2\) 

\(\sqrt{\frac{M_s}{m_p}}=\frac{r_p}{r_H}-1\)

\(r_H=\frac{r_p}{1+\sqrt{\frac{M_s}{m_p}}}\)

b) Planetary Hill radii: Calculate the Hill radii for Earth, Jupiter, and Neptune. How do they compare with the separation between the planets and their most distant moons?

We can use the table above to calculate the Hill radii for Earth, Jupiter, and Neptune. Since the masses are given to us in terms of Earth masses, it's helpful to know that the Sun is 333,000 times as massive as Earth. 

\(r_{H(Earth)}=\frac{1AU}{1+\sqrt{\frac{3.33\times10^5M_\oplus}{1M_\oplus}}}=0.0017AU=2.59\times10^{5}km\)

\(r_{H(Jupiter)}=\frac{5AU}{1+\sqrt{\frac{3.33\times10^5M_\oplus}{320M_\oplus}}}=0.150AU=2.25\times10^{7}km\)

\(r_{H(Neptune)}=\frac{30AU}{1+\sqrt{\frac{3.33\times10^5M_\oplus}{17M_\oplus}}}=0.213AU=3.18\times10^{7}km\)

These numbers are fairly consistent with the observed moon distances for Earth, Jupiter, and Neptune. 

Week 10: WS17 #2

2. The Minimum Mass Solar Nebula (MMSN): The MMSN is the minimum mass protoplanetary disk that could have produced the Solar System. In this problem we will calculate it with increasing detail. Table 1 provides the current locations and compositions of the Solar System planets, as well as the original composition (estimated from the present day composition of the Sun). 

a) Single planet-based estimate: How many Jupiter masses in original Solar Nebula material would it have taken to build up the present day Jupiter? 

First we have to figure out the "limiting reactant" in Jupiter's formation. We can do this by taking the ratio of Jupiter's composition to the Sun's composition for each individual component. 

H, He: \(\frac{93}{98.4}=0.95\)

C, N, O: \(\frac{6}{1.2}=5\)

Si, Mg, Fe...: \(\frac{1}{0.3}=3.33\)

Since the ratio is greatest for C, N, and O, these are the limiting reactants, and 5 times Jupiter's mass would be required in order to achieve high enough concentrations of those atoms to form the planet. Knowing that the Sun has a mass of \(3.33\times10^5M_\oplus\), we can calculate that mass in solar masses: 

\(\frac{5M_J}{1}\frac{320M_\oplus}{1M_J}\frac{1M_\odot}{3.33\times10^5M_\oplus}=4.8\times10^{-3}M_\odot\)

b) Planet-mass-based estimate: Make a table of the 8 planets. For each planet, calculate how many planet-masses of nebular material would have been needed to make that planet. Add another column with the mass of nebular material needed for each planet (in Solar masses). Which planet is the most important to consider for estimating the minimum mass of the Solar Nebula? What is the total (order of magnitude) minimum mass of the Solar Nebula taking into account all planets? 

The steps for the other planets follow the same order as what we just calculated for Jupiter: use ratios to figure out the limiting reactant and the number of planetary masses, and then convert to solar masses. The solutions for each planet are summarized in the table below. 

Planet	Distance (AU)	Mass (\(M_\oplus\))	Limiting reactant	Material needed (\(M_{planet}\))	Material needed (\(M_\odot\))
Mercury	0.4	0.06	Si, Mg, Fe…	333	6.00E-05
Venus	0.7	0.8	Si, Mg, Fe…	233	5.60E-04
Earth	1	1	Si, Mg, Fe…	233	7.00E-04
Mars	1.5	0.11	Si, Mg, Fe…	233	7.70E-05
Jupiter	5	320	C, N, O	5	4.80E-03
Saturn	9.6	95	C, N, O	6.67	1.90E-03
Uranus	19	15	C, N, O	58.3	2.63E-03
Neptune	30	17	C, N, O	70	3.57E-03

The total material needed is on the order of 10^-2 solar masses, about a third of which is contributed by Jupiter. 

c) Nebular surface density: The surface density describes the amount of material available to form a planet at a specific location assuming that a planet can accrete material regardless of how high up in the disk it is. In this problem we will calculate what the required surface density profile of the MMSN was to form the present-day Solar System. To achieve this, we will take the masses from (b) and distribute these minimum mass requirements over a series of annuli, centered on each planet. Choose boundaries of annuli to be halfway between the orbits of each planet. In the case of Mercury we would estimate that it formed from material within an annulus of 0.4±0.15AU. The surface density of an annulus is mass/area. Calculate the surface density needed for each planet in g/cm². Make a plot of surface density vs. radius. Notice a trend? Any deviations from that trend? How much does the surface density requirement decrease between 1 and 5 AU? Between 5 and 30 AU? 

In order to calculate the surface density, you need the inner and outer radii of each planet's annuli in order to calculate the area. You can then divide the mass, calculated above, by the area. For Mercury, we know that its reach is from 0.25-0.55AU. 

\(A_{Mercury}=\pi(0.55^2-0.25^2)=0.754AU^2\)

\(\frac{0.754AU^2}{1}(\frac{1.496\times10^{13}cm}{1AU})^2=1.69\times10^{26}cm^2\)

\(SD_{Mercury}=\frac{(6\times10^{-5}M_\odot)(2\times10^{33}g/M_\odot)}{1.69\times10^{26}cm^2}=711g/cm^2\)

The calculations for the other planets are summarized in the table below. 

Planet	Distance (AU)	Material needed (\(M_\odot\))	Annuli (AU)	Area (cm2)	Surface density (g/cm2)
Mercury	0.4	6.00E-05	0.25	1.69E+26	712
Venus	0.7	5.60E-04	0.55	2.95E+26	3793
Earth	1	7.00E-04	0.85	5.90E+26	2371
Mars	1.5	7.70E-05	1.25	6.32E+27	24
Jupiter	5	4.80E-03	3.25	3.00E+28	320
Saturn	9.6	1.90E-03	7.3	1.06E+29	36
Uranus	19	2.63E-03	14.3	2.78E+29	19
Neptune	30	3.57E-03	24.5	4.64E+29	15
			35.5

Plotting surface density vs. radius gives us this plot: 

Aside from Mercury and Mars which have very low surface densities, the trend looks like an exponential decay curve. There is a steep decline between 0 and 5 AU, with the surface density remaining relatively constant between 5 and 30 AU. 

d) A widely used expression for MMSN is \(1700(\frac{r}{1AU})^{-1.5}g/cm^2\). How does this expression compare with your answer in (c)? 

Plotting the planets based on this expression (orange) compared to what we calculated (blue) gives us this graph: 

They look pretty close, but I think it's easier to see the fit with a graph of the log of the surface density: 

Mercury and Mars are still outliers, but the trendlines are pretty similar. 

Week 9: That's Ms. Dr. Astronaut to You

The most recent group of NASA astronauts is Group 21. The eight astronauts in the program were selected from over 6,300 applicants (an admit rate that makes me feel a bit better about the low acceptance rates at Harvard Med), and are split evenly between men and women. Six of the eight are officers in the armed forces, and most importantly, one of them, Major Andrew R. Morgan, is an emergency physician--which is what I want to do.

Over 20 astronauts in NASA's history who have participated in space missions have also been doctors. Doctors are important on these missions for several reasons. First, NASA conducts biomedical research in space to better understand a range of phenomena from muscle wasting diseases to gene expression to cell growth in microgravity. A physician's perspective (especially if that person also has experience with basic research) can be important in the execution and interpretation of the data generated. Second, space is not exactly the ideal environment for the human body, but it's vital that astronauts stay healthy. While I'm sure all astronauts undergo training and understand what can happen to their bodies when they're not on Earth, this is mostly in the intellectual realm of the doctors. Finally, people can get sick during space missions. Even a minor ailment deserves attention so that all of the crew can be working at peak efficiency.

Routine check-ups....in space!

However, NASA doesn't require that a doctor be on each mission. Instead, the rest of the crew receives some basic medical training, and in all of the missions that have been attempted so far, contact with physicians on the ground and early return have both been available options--although early return has never been necessary. This makes a lot of sense for shorter trips that are close to the Earth, such as trips to the ISS (which is much, much closer than the Moon). If NASA plans any longer trips, however, doctors will become much more important. First of all, there will be no opportunity to turn around if a crew member needs an appendectomy halfway to Mars, and communication with Earth can be spotty or delayed too. Secondly, longer periods of space travel mean more intense physical effects than shorter flights. Muscle decay, cardiac shrinkage, and weakened bones become even more of a problem for someone in space for a couple of years than someone in space for a couple of months.

In some ways, it doesn't make sense for there to be only one doctor on extended missions--what if something happens to the only doctor in the first half of the mission? While the vehicle and its equipment are expensive (like really expensive), the astronauts themselves arguably make up the bulk of the investment, so their health and physical integrity should be just as double- and triple- and quadruple-ensured as anything else on board. Obviously the number of doctors in a crew depends in part on the crew's size--you probably don't need five physicians for a six-person mission--but all other things being equal, more doctors seems better to me. And I'm not just saying that for the sake of my own astronaut application when the time comes.

I have no idea what this is, but it will be me someday.

Sources 
https://en.wikipedia.org/wiki/NASA_Astronaut_Group_21
http://www.nasa.gov/astronauts/2013astroclass.html
http://www.nasa.gov/astronauts/2013_morgan.html
http://www.amednews.com/article/20100315/profession/303159950/4/
https://www.nasa.gov/ames/research/space-biosciences/rodent-research-3-spacex-8
https://www.nasa.gov/ames/research/space-biosciences/wetlab-2-spacex-8
http://www.spacepolicyonline.com/news/nasa-ig-iss-cost-u-s-75-billion-so-far-estimates-of-future-costs-overly-optimistic
http://36.media.tumblr.com/73a703b55ba830d342d5f3086a84c12e/tumblr_n1vhkqBWce1rfn5l1o1_1280.jpg
http://media2.s-nbcnews.com/j/msnbc/Components/Photos/060217/060217_SL2-02-157_hmed_1p.grid-6x2.jpg

Week 9: WS16 #1

1. Forming stars: Giant molecular clouds occasionally collapse under their own gravity (their own "weight") to form stars. This collapse is temporarily held at bay by the internal gas pressure of the cloud, which can be approximated as an ideal gas such that P=nkT, where n is the number density (cm^-3) of gas particles within a cloud of mass M comprising particles of mass \(\bar{m}\) (mostly hydrogen molecules), and k is the Boltzmann constant, k=1.4x10^-16erg/K.  
a) For a spherical molecular cloud of mass M, temperature T, and radius R, relate the total thermal energy to the binding energy using the Virial Theorem, recalling that you used something similar to kinetic energy to get the thermal energy earlier. (Hint: a particle moving in the i^th direction has \(E_{thermal}=\frac{1}{2}mv_i^2=\frac{1}{2}kT\). This fact is a consequence of a useful result called the Equipartition Theorem.) 

The Virial Theorem states that \(-\frac{1}{2}U=K\). Based on results for potential energy from previous worksheets, this means that \(\frac{1}{2}\frac{3}{5}\frac{GM^2}{R}=\frac{3}{2}kT\frac{M}{\bar{m}}\). The kinetic energy is multiplied by 3 because it has 3 degrees of freedom, and by the number of particles (total mass divided by average particle mass) to calculate the energy for the total system.
\(\frac{GM}{5R}=\frac{kT}{\bar{m}}\)

b) If the cloud is stable, then the Virial Theorem will hold. What happens when the gravitational binding energy is greater than the thermal (kinetic) energy of the cloud? 

The cloud will collapse under its own weight because there won't be enough kinetic energy to prevent the matter from coalescing.

c) What is the critical mass, M_J, beyond which the cloud collapses? This is known as the "Jeans Mass." Assume a cloud of constant density \(\rho\). 

When solving for the critical mass, we want to eliminate radius and express the answer in terms of density instead. Solving the equation from part (a) for M gives us \(M=\frac{kT}{\bar{m}}\frac{5R}{G}\), plugging in \(R=(\frac{3}{4}\frac{M}{\pi\rho})^{1/3}\), and solving for M again yields the Jeans Mass.
\(M=(\frac{kT}{\bar{m}}\frac{5}{G}(\frac{3M}{4\pi\rho})^{1/3}\)
\(M_J=(\frac{5kT}{G\bar{m}})^{3/2}(\frac{3}{4\pi\rho})^{1/2}\)

d) What is the critical radius, R_J, that the cloud can have before it collapses? This is know as the "Jeans Length." 

We want to express the Jeans Length in terms of density rather than radius, so we plug \(M=\frac{4}{3}R^3\rho\) into \(\frac{GM}{5R}=\frac{kT}{\bar{m}}\) and solve for R.
\(R=\frac{G(\frac{4}{3}\pi R^3\rho)\bar{m}}{5kT}\)
\(R_J=\sqrt{\frac{15kT}{4\pi G\rho\bar{m}}}\)

e) The time for a self-gravitating cloud to collapse is often estimated by the "free-fall timescale," or the time it would take a cloud to collapse to a point in the absence of any resistance. We'll derive this timescale and use it to re-derive the Jeans Length. Consider a test particle in an \(e\approx1\) orbit around a point mass equal to the cloud's mass. The time it takes for a point mass to move from R to the central mass, or half an orbit, is equivalent to the free-fall timescale. Use \(M=\frac{4}{3}\pi R^3\rho\) to frame this expression in terms of a single variable--the average density \(\bar{\rho}\). \[t_{ff}=\sqrt{\frac{3\pi}{32G\rho}}\]

This time is equal to half the period of the particle's orbit--even though an ellipticity of 1 means that the particle is moving in a straight line. We can use Kepler's Law to solve this.
\(\tau=P/2=\frac{1}{2}\sqrt{\frac{4\pi^2a^3}{GM}}\)
As the semimajor axis, a is half the radius. We also want to solve this in terms of density rather than mass.
\(\tau=\frac{1}{2}\sqrt{\frac{4\pi^2(R/2)^3}{G\frac{4}{3}\pi R^3\rho}}=\sqrt{\frac{3\pi}{32G\rho}}\)

f) If the free-fall timescale of a cloud is significantly less than a "dynamical timescale," or the time it takes for a pressure wave (sound wave with speed c_s) to traverse the cloud, the cloud will be unstable to gravitational collapse. Use dimensional analysis to derive the relationship between the sound speed, the cloud's pressure P, and the mean density. Then derive the dynamical timescale, the time it takes a pressure wave to cross the cloud of radius R. 

\(P=[\frac{g}{s^2cm}]\)
\(c_s=[\frac{cm}{s}]\)
\(\bar{\rho}=[\frac{g}{cm^3}]\)
Based on these units, the relation is \(c_s=\sqrt{\frac{P}{\bar{\rho}}}\).
The time it takes to travel a distance R at the speed of sound is \(t=\frac{R}{c_s}=\frac{R}{\sqrt{P/\bar{\rho}}}\).

g) Equate the free fall time to the sound crossing time and solve for the maximum R. This maximum is the Jeans Length, R_J, which we derived previously. Use the ideal gas law to ascertain that the two equations for Jeans Length match, at least if we neglect constants of order unity due to assumptions of the system's geometry. 

\(\sqrt{\frac{3\pi}{32G\rho}}=R\sqrt{\frac{P}{\bar{\rho}}}\)
\(R_{max}=\sqrt{\frac{3\pi P}{32G\rho^2}}\)
The ideal gas law tells us that \(P=nkT\). Since number density can also be expressed as density divided by particle mass, we can say \(P=\frac{\rho kT}{\bar{m}}\).
\(R^2=\frac{3\pi\rho kT}{32G\rho\bar{m}}\)
\(R=\sqrt{\frac{3\pi kT}{32G\rho\bar{m}}}\)
If we eliminate the constants from both this radius and the Jeans Radius we calculated in part (d), we get \(\sqrt{\frac{kT}{G\rho\bar{m}}}\) for both.

h) For simplicity, consider a spherical cloud collapsing isothermically (constant temperature, T) with initial radius R₀ = R_J. Once the cloud radius reaches 0.5R₀, by what fractional amount has R_J changed? What might this mean in terms of the number of stars formed within a collapsing molecular cloud? (This is the concept of fragmentation.) 

Since density changes with the cube root of the radius, halving the radius will multiply the density by 8. In the Jeans Radius equation, if density increases by a factor of 8, R_J will change by a factor of \(\sqrt{\frac{1}{8}}\). This indicates that the Jeans Radius will decrease faster than the radius of the cloud. The matter within the miniature Jeans Radii can then undergo collapse themselves. This means that multiple individual stars may collapse from a single cloud.

Week 9: WS15 #1

1. a) Hydrogen energy levels: Outside of molecular clouds, the most abundant species in the interstellar medium (ISM) is atomic hydrogen (in molecular clouds it is molecular hydrogen). Whether the ISM is fully ionized or not will therefore depend on how easily atomic hydrogen is ionized. The ground electronic state of a hydrogen atom corresponds to an atom with the smallest (and hence most tightly bound) electron orbit around the nuclear proton that is consistent with a stationary electronic wave function (a standing wave). The electronic energy levels permitted by quantum mechanics are characterized by their quantum numbers n=1 2 3, where n=1 corresponds to the ground state. Make a drawing of the electronic energy levels of atomic hydrogen. Mark out the energy needed to excite an atom in its ground state to a free proton and electron. Illustrate what happens in the case of photoionization. 

Ideally a hydrogen atom will not resemble an avocado as much as this one does. 

The energy required to ionize a hydrogen atom is 13.6eV. If a photon of this energy is absorbed, the electron will jump from the ground state, n=1, to n=\(\infty\) and be freed from the proton.


b) Ionizing stars: Remember that stars are blackbodies. Which kind of stars emit a majority of their photons with energies high enough to photoionize (excite an electron into freedom) ground state hydrogen? Give your answer in both stellar surface temperature and letter classification. 

The ionization energy of a ground-state electron in a hydrogen atom is 13.6eV, which is equivalent to 2.18x10^-11erg. We can use this to calculate the wavelength of the ionizing photon.
\(E=hc/\lambda\)
\(\lambda=hc/E\)
\(\lambda=\frac{(6.626\times10^{-27}erg.s)(3.0\times10{10}cm/s)}{2.18\times10^{-11}erg}=9.11\times10^{-6}cm\)
We can now calculate the temperature of the star that releases photons of this wavelength.
\(\lambda_{max}=b/T\)
\(T=b/\lambda_{max}\)
\(T=\frac{0.290cmK}{9.11\times10^{-6}cm}\approx32,000K\)
This corresponds to O-type stars, the hottest stars.

c) Excitation state of hydrogen: But why do we only care about excitation from the ground state to free protons and electron? After all, if hydrogen is in an excited state (eg. n=2) you could use many more of the available stellar photons to ionize the ISM. The lifetime of an excited state is ~ 10⁹s. Let's calculate the time scale of ionization right next to the star to test whether it is reasonable to assume that all hydrogen are in their ground state. First, set up an equation for the ionization rate for a single hydrogen atom in terms of the photon flux and the ionization cross section \(\sigma\). The ionization cross section is 10^-17 cm². Calculate the photon flux assuming that you are sitting right next to the star from (b) and that the star is emitting all its energy in the form of photons with the exact energy required to ionize the atomic hydrogen. 
How do the two time scales compare? Is it reasonable to assume that all hydrogen is in the ground state? 

We can calculate the photon flux by dividing the total flux by the energy per photon:
\(F_\gamma=\frac{\sigma_{SB}T^4}{2.18\times10^{-11}erg}=\frac{(5.67\times10^{-5}erg/cm^2s)(32000K)^4}{2.18\times10^{-11}erg}=2.73\times10^7/cm^2s\)
The dimensions of photon flux are photons per time per area, so to get the rate, we multiply by the cross section: \(F_\gamma \sigma=(2.73\times10^7/cm^2s)(10^{-17}cm^2)=2.73\times10^7/s\).
By inverting this, we can calculate the ionization timescale: \(3.67\times10^{-8}s\). This is longer than the timescale of the excited electron by about one order of magnitude. This means that it is reasonable to assume that all hydrogen is in the ground state--it will return from the excited state to the ground state much faster than it will be re-ionized.

d) Recombination: The inverse of photoionization is recombination. In a recombination event, an electron and proton collide and become bound while emitting a photon. Illustrate a recombination event. Set up an equation for the recombination rate in terms of the number densities of protons, electrons, and the rate coefficient \(\alpha\), which describes the efficiency at which a recombination occurs when an electron and proton collide. Note that a recombination can happen to any hydrogen energy level. If the recombination takes the hydrogen immediately to the ground state you will produce a new ionizing photon. If the recombination takes the hydrogen into any other level, the emitted photon will not be able to ionize another hydrogen atom. 

The photon will be emitted as the proton and electron combine. This rate is given by \(r=\alpha n_pn_e\) where \(n_p\) is the number density of protons and \(n_e\) is the number density of electrons. 

Week 9: Orion

My favorite constellation is Orion. Probably the main reason for this is that it's the only one I can reliably find (I can't even find the Big Dipper sometimes...). When I was in Chile a year or so ago, I watched him move across the sky every night as I enjoyed the Chilean summer, music, and company.

This just goes to show that you can be an excellent warrior without really having a head.

The seven most distinct stars that make up the constellation form the body and belt of Orion, who is a hunter. Something that I didn't know about Orion is that his shoulders are formed by the stars Betelgeuse (which immediately reminds me of Hitchhiker's Guide to the Galaxy) and Bellatrix (which immediately reminds me of Harry Potter). Less prominent stars form his arms and his shield (plot twist--it's not a bow like I always thought, even though I feel like a bow would make more sense for a hunter to have than a shield). Finally, two stars and the Orion Nebula form the sword that hangs down from his belt. 

The Orion Nebula, which is about 1,300 lightyears away, is one of a few nebulae that are visible to the naked eye. This formation has been greatly studied and has helped astronomers understand star formation and evolution of molecular clouds. Its core is formed by large O-class stars, which contribute a blue color to the nebula. Interestingly, a green color emitted by the nebula is caused by an electron transition in oxygen ions believed impossible for a long time. 

The Orion Nebula

Sources 

http://pages.cs.wisc.edu/~arun/orion/OrionPic.jpg

https://en.wikipedia.org/wiki/Orion_(constellation)
https://en.wikipedia.org/wiki/Orion_Nebula
http://www.astrocruise.com/milky_way/M42_0712.jpg

Week 9: An Introduction to Modern Astrophysics Ch23

This chapter of An Introduction to Modern Astrophysics covered planet formation in our solar system and beyond. It overviewed how stars and planets form, metallicities, and a brief overview on exoplanet detection, among other things. One of the topics that I thought was interesting was how the composition of planets in our solar system was determined. I knew that there are both gaseous and rocky planets in our solar system, but I didn't really know why they were ordered in the way they are or how each came to be one or the other.

The most widely accepted theory for planetary formation is that they condensed from the "leftover" material after the Sun collapsed from a cloud of gas and dust. One reason that has been proposed for why the planets are composed of different material from each other and from the Sun is that somehow a gradient formed, both in terms of the composition and the temperature of the protoplanetary disc. This meant that different materials could condense at different distances from the Sun. Jupiter, for instance, was at a distance where it was cold enough that ice particles could condense and add to the growing planet. This region was also close enough to the Sun that the protoplanetary disc was fairly dense. This allowed Jupiter to get even bigger until it was large enough to attract the lower-mass gas particles in the area, ultimately becoming the gas giant we know and love.

Another factor that played into many of our solar system's characteristics is bombardment by smaller objects. A widely accepted theory to explain the formation of our Moon is that an object about the size of Mars collided with the Earth, releasing a substantial amount material into orbit around the Earth. This material ultimately condensed and formed the Moon. Collisions can also explain why some planets (Venus and Uranus) don't rotate in the same way as all the other planets--collisions with other objects in the solar system could have altered their rotations.

The formation of our solar system even included other craziness like ejection of planetesimals from the Sun's orbit, gravitational resonance, and migration of planets inwards--but that's a story for another time.



Sources 
http://acolwell.wikispaces.com/file/view/Inner_Rocky_and_Outer_Gas_Planets.gif/538464050/Inner_Rocky_and_Outer_Gas_Planets.gif
An Introduction to Modern Astrophysics, Carroll & Ostlie 
https://en.wikipedia.org/wiki/Moon
http://www.ucolick.org/~mountain/AAA/aaawiki/doku.php?id=why_do_some_planets_have_reverse_rotation